Laurent Jaeken*1 and Vladimir Vasilievich Matveev2
1Laboratory
of Biochemistry, Karel de Grote University College, Department of
Applied Engineering, Salesianenlaan 30, B-2660, Antwerp, Belgium
2Laboratory of
Cell Physiology, Institute of Cytology, Russian Academy of Sciences,
Tikhoretsky Ave 4, St. Petersburg 194064, Russia
*Address correspondence to this author at the
Laboratory of Biochemistry, Karel de Grote University College,
Department of Applied Engineering, Salesianenlaan 30, B-2660, Antwerp,
Belgium; Tel:+1323 663 30 31; Fax: +1323 293 34 08;
Emails:
laurentjaeken@hotmail.com;
laurentjaeken@kdg.be
Keywords: Entropy, coherence, polarized water, unfolded proteins, native aggregation, association-induction hypothesis.
Full text [PDF]
Abstract. Observations of coherent cellular behavior cannot be integrated into widely accepted membrane (pump) theory (MT) and its steady state energetics because of the thermal noise of assumed ordinary cell water and freely soluble cyto-plasmic K+. However, Ling disproved MT and proposed an alternative based on coherence, showing that rest (R) and ac-tion (A) are two different phases of protoplasm with different energy levels. The R-state is a coherent metastable low-entropy state as water and K+ are bound to unfolded proteins. The A-state is the higher-entropy state because water and K+ are free. The R-to-A phase transition is regarded as a mechanism to release energy for biological work, replacing the clas-sical concept of high-energy bonds. Subsequent inactivation during the endergonic A-to-R phase transition needs an input of metabolic energy to restore the low entropy R-state. Matveevís native aggregation hypothesis allows to integrate the energetic details of globular proteins into this view.
Introduction. Among physicists there have always been people who are interested in basic physical approaches to the phenomena of life. Unlike mathematics, physics always requires models or mechanisms without which the tools of the discipline are not applicable. Cell physiology has suggested two opposing models of the living cell to physicists: (i) a cell is a membrane-delineated bubble with an electrolyte solution inside; (ii) a cell is a different phase relative to the surrounding fluid. The main difference between these models is in the physical state of intracellular water and K+ (the main cation of the cell). For the first model, water and K+ are free in the cell. Membrane (pump) theory (MT) was founded on this basis [1-7]. It describes a large set of interrelated physiological phenomena (solute distribution, transport across membranes, cell potentials, osmotic behavior, aspects of motility, etc.). One of its basic concepts, that of the Na+/K+ pump using a continuous energy supply from the hydrolysis of the high-energy bond of ATP [8], is intimately linked with that of steady state energetics; the metaphor that life can be com-pared to a burning candle. In contrast, the idea that a cell is a different phase forms the basis for a number of bulk-phase theories [9-15] describing the same physiological phenomena in a completely different way. According to the latter, water and K+ are bound in the cell and the protoplasm resembles a drop of gel.
Of course, these fundamentally different models require very different physical approaches. MT failed to offer key ideas for creating a general physical approach to the cell. Instead, various specific questions were subjected to physical analysis such as the explanations for membrane potential, muscle contraction, protein conformation, etc [16]. However, these fragments of knowledge cannot be assembled into a holistic theory of the cell. The separate topics are like the reflections of a whole cell in a broken mirror of physics. The fragments were obtained by different authors using different physical approaches, often contradicting each other. On the other hand, Schrödinger [17] proposed a unified view of the cell, but his ideas had little effect on cell physiology and were discussed mainly among physicists. In our opinion, this is because MT has the widest following among physiologists and the broader interdisciplinary area of biology. Unfortunately, MT proved to be incompatible with the scale of Schrödinger's ideas. We would like to show that Schrödinger's ideas are fully compatible with the bulk-phase model of the cell. But this will entrain another model for cell energetics.
Ling's Association-Induction Hypothesis (AIH) [11, 12, 18-26] is the supreme achievement of the bulk-phase approach to physiological phenomena in the living cell. According to Ling, the cell is a holistic system because water and K+ are adsorbed to a matrix of cell proteins making that these three physiologically relevant components act as a single whole. Owing to a network of proteins with natively unfolded conformation, which strongly binds, orients and polarizes water, the cell acquires the capacity for coherent behavior. Since water is bound, limited in motion and ordered in space, the entropy of the cell is lower than in a cell with free water. The entropic contribution of water is very important because water makes up most of the mass of the cell (its intracellular concentration is about 44 M). The bound state of K+ is another contribution to the reduction of entropy. Furthermore, the presence of a network of interconnected protein molecules, called Ďcell matrixí, reduces the entropy of the protein component of the system. All these features are inherent to the cell during the resting state (R-state): relaxed myofibrils, resting potential, inactive secretion processes, unfertilized egg, dormant spores and cysts, etc. So, the cell during the R-state is a protein-water-K+ complex having cooperative properties. This complex appears as a single coherent whole.
During the protoplasmic phase transition from the R-state to an active state (A-state), the complex is transformed and water and K+ become free. The entropy of the system increases. The free energy of the system is reduced (because of the entropic contribution). The released energy is utilized for biological work: myofibril contraction, action potential, secretion, fertilization, germination, etc. Thus, in this view, entropy plays a key role in cell energetics, which makes Ling's cell model qualitatively compatible with Schrödinger's view.
The physical concept of phase transition is not sufficiently detailed to serve as an adequate account of cell physiology. However, the recently published [15] native aggregation hypothesis (NAH) provides specific physiological and biochemical details. During the R-to-A phase transition, natively unfolded proteins form temporary secondary structures that interact only with secondary structures complementary to them. Natively unfolded and globular proteins temporarily form new active functional systems. The energetic aspects of this process are the immediate objective of this article. We believe that a mechanism of energy transformation in the living cell (its release and utilization) must include a change in the sorption properties of proteins as a key event. Water and K+ ions are the main adsorbents in this mechanism. ATP is seen as the regulator of the sorption properties of proteins. The source of energy for biological work is not ATP alone but supra-molecular ATP-protein-water-K+ complexes with an ordered structure and coherent properties.
Our larger goal is to attract the attention of physicists, physical chemists, cell biologists and biochemists to the problems discussed. We hope to offer a new synthesis of ideas from different scientific disciplines. This is the time to join forces.
1. The Origin of Generally Accepted Membrane Theory (MT)
In 1930 a crucial experiment by the famous physiologist A.V. Hill [2, 3] seemed to lay down the basis of Ďmembrane (pump) theoryí (MT). This theory holds (a) that cells are delineated by an intact plasma membrane separating the external solution of ions and other solutes from the cytoplasmic solution and (b) that the plasma membrane exerts some pumping activity, thought to be responsible for the observed concentration gradients of ions, which are not in thermodynamic equilibrium when calculated using the law of Nernst. (c) This non-equilibrium situation leads to steady state cell energetics, in which metabolism-dependent pumping unceasingly compensates for passive leaks.
Before 1930, ideas in the realm of MT were rivaled by bulk-phase theories, in which the colloid phase of the cytoplasm was thought to be responsible for concentration differences between a cellís interior and its surroundings. In order to stop the endless debate, Hill [2] determined the distribution coefficient of a neutral molecule, urea, between the cytoplasm of resting muscle cells and the Ringer solution in which they were bathed. He found it to be close to one. Hence he concluded that intracellular water has similar properties to the water outside the cell. He also concluded that in order to explain the measured osmotic pressure [3], the most abundant intracellular ion (K+) must be in solution. These inferences seemed to oppose the possibility of a colloidal cytoplasm. They implied that the aqueous environment inside a cell must be a solution and hence the law of Nernst should be applied. This led to the conclusions that membrane pumps must exist and that the cell exhibits steady state energetics. Hillís experiment caused most proponents of bulk-phase theories to adopt MT instead.
In 1957 Skou [27: review] discovered that the plasma membrane protein Na+/K+-ATPase shared some key properties with the physiological process of active Na+ and K+ transport, suggesting that this membrane-located enzyme is in fact the Na+/K+ pump. But it took much additional research before general agreement was reached. Hoffman [28] confirmed that ATP was indeed the direct metabolic intermediate. From the then-popular view of Lipmann [8], it followed that hydrolysis of the high-energy bond of ATP would act as an instantaneous injector of energy into the pump. Reconstitution of the purified Na+/K+-ATPase into phospholipid vesicles by Hilden et al., [29] in 1974 is generally considered as definite proof of the pumping activity of this enzyme. A year later, Glynn and Karlish [30] wrote a much cited review of all the work done up to then, unfortunately without mentioning an important alternative explanation, the Ďassociation-induction hypothesisí (AIH), worked out by Ling during the preceding decade [11] and presented at an international conference two years earlier [31, 32]. While Lingís alternative has remained virtually unknown Ė but to date also un-refuted Ė MT quickly developed into an unquestioned paradigm, appearing as the only explanation for a large number of interconnected physiological phenomena. It seemed to explain non-equilibrium gradients and the transport of ions and other solutes by the direct action of membrane-located pumps and indirectly by coupled transport mechanisms [33] (for another explanation see [12, 18, 19]; for trans-epithelial transport see [18, 34]). By showing how concentrations of low molecular mass solutes could be kept in steady state, an explanation for osmotic balance and hence cell volume was given [27] (for another explanation see [11, 14, 18, 19]). The electric imbalance of pumping 3 Na+ outwards in exchange for 2 K+ inwards [35] was taken as an explanation for the existence and the observed value (-70 mV in neurons) of the resting potential and seemed to elucidate the property of excitability of some cell types [7] (for other explanations see [11, 14, 18, 19, 36-39]). Respiration-dependent proton transport in mitochondria and bacteria and light-driven proton transport between internal and external bulk phases were considered to energize membrane-dependent ATP synthesis in these organelles and in bacteria by means of chemiosmosis [40] (for other explanations see [18, 41-44]). Clearly, the idea of membrane-located ion-pumps became central to a large and very central part of classical cell physiology, despite many criticisms from many different fronts. Two recent reviews cover the present status and historical development of this issue: one by Ling [25] discussing the proís and contraís of both MT and its alternative (AIH); the other by Glynn [45], who unfortunately continues to discuss only MT.
2. The Problem with MT
Three kinds of observations opposing MT and its steady state energetics are selected here from a much broader context (see [25] for a historical review). They are: (a) the rapidly increasing number of observations supporting the coherent behavior of life; (b) the abundant evidence that cell water is largely structured; and (c) the abundant evidence that cellular K+ is mostly in a bound (adsorbed) state. These three kinds of observations are directly interlinked because the adsorption properties of (some) proteins for water and K+ ensure coherent behavior and a high degree of order down to the molecular level. The disorder due to free water (about 44 M) and free K+ (about 0.15 M), as MT protagonists contend, would not support most of the coherent processes. There is an additional link between the state of water and that of K+, already given in the discussion of the experiments of Hill. The measured osmotic pressure of the muscle cells in Hillís experiment can be explained in two ways. When water is free, this implies that there is no colloid and hence no colloid osmotic pressure. Then there is just the normal osmotic pressure of the proteins and this is not sufficient. Therefore, the main intracellular solute K+ (about 0,150 M) must also be osmotically active, i.e. it must be free. In contrast, when water is structured, there must be a colloid phase and colloids have an osmotic pressure which is much higher than expected on behalf of their molar activity (sometimes called colloid osmotic pressure), and which for cells almost on its own explains the measured osmotic pressure [12, 18, 19]. Hence, K+ should be osmotically inactive by being bound. Observations during the past 50 years culminated in favor of the second possibility. But how then should the findings of Hill be explained?
In 1973, Ling et al., [31] confirmed after the experiment of Hill, but also performed a large number of similar experiments using many solutes other than urea. They found that distribution coefficients for substances as small as urea are indeed close to one, but for larger neutral molecules they are definitely below unity: the larger the molecule, the lower the coefficient. It became clear that Hillís choice of urea had been quite unfortunate (and is an example of the serious errors to which the most reputable scientists can be prone). The much more elaborate studies of Ling et al., [32] (many other substances were tested later [11, 18-20]) led to the opposite conclusions: (a) intracellular water cannot be ordinary water and must be structured, (b) intracellular K+ cannot be in solution but must be largely bound, and (c) cytoplasm must be colloid-like, possessing solvencies that are quite different from those in ordinary water. Among the solutes studied were sodium salts. The distribution coefficient for Na+ was shown to explain its gradient fully without the need for pumping [11, 18-20, 25]. The structured and polarized state of almost all cellular water and the physical state of the intracellular K+ as largely adsorbed were both demonstrated using a wide variety of modern techniques. A brief overview of some major pieces of evidence will be given in the next two sections.
3. The Polarized State of Cellular Water
Early ideas about bound water failed because of the lack of a physical theory describing such water at the molecular level. In 1965, Ling [46] developed such a theory and made it part of his AIH. Briefly, it states that a surface, for instance a polymer matrix, is able to orient and electrically polarize the dynamic structure of water when it bears an appropriately spaced checkerboard pattern of sufficiently strong positive (P) charges (these may be partial positive charges such as on ĖNH groups) in regular alternation with sufficiently strong negative (N) charges (these may be partial negative charges such as on ĖCO groups) together forming a so-called ĎNP-NP-systemí; or a comparable pattern of alternating (partial) positive (P) and neutral (0) sites forming a ĎP0-P0-systemí, or alternating (partial) negative (N) and neutral (0) sites forming a ĎN0-N0-systemí. The water molecules in close contact with the polymer will be spatially oriented by the polymer charges, but in addition, the stronger dipoles of the polymer will induce a greater dipole moment in the water molecules, so that the latter also become electrically polarized. In consequence, the dipole moment of the adsorbed water is higher than that of bulk water. The result is that further layers of water are induced one after the other. Ling [46] called this Polarized Multi-Layer water or PML-water. It exhibits long-range dynamic structuring. The higher total dipole moment stabilizes the multi-layers because it leads to stronger hydrogen bonds and this makes it a poor solvent for most solutes that are highly soluble in normal (bulk) water. Translational as well as rotational freedom of the water molecules is reduced and the residence time of each water molecule at a specific location is increased. Together, this makes all the physicochemical properties of PML-water differ from those of normal water. And this is the way to test the presence of PML-water in cells. The aberrant properties of PML-water were first studied in inanimate model systems of suitable polymers and then compared with the properties of cell water [11, 18-21]. The results obtained from this approach as well as an updated theoretical background were recently reviewed [20].
An important question concerns the thickness of the oriented-polarized multilayers. Giguère and Harvey [47] studied a water film between two parallel polished AgCl plates at a distance of 10 μm and unexpectedly found that it did not freeze even at -176 ?oC. The infrared absorption spectrum was indistinguishable from that at 31 ?oC. This means that about 30,000 layers of water molecules are involved. The experiment was highly reproducible, indicating that the situation represents a true equilibrium state and not just a metastable equilibrium as in the case of supercooling. More recently, Ise et al., ([48], see also [49]) obtained striking micro-cinematography of latex particles suspended in both ordered and disordered water, revealing long stochastic trajectories for the latter, as might be expected from Brownian motion, and a tetragonal quasi-crystalline pattern of particles almost free of movement for the former. This is remarkable because the individual particles are situated several micrometers from each other, yet are ordered in a tetragonal pattern. Moreover, experiments by Zheng and Pollack ([50], see also [49]) generated water polarization up to hundreds of micrometers away from the surfaces of hydrophilic gels and of muscle preparations. All three of these sets of observations support Lingís conclusion [20] that an idealized system may enhance water-to-water adsorption energy ad infinitum.
Applying his theory of NP-NP-systems to cells, Ling [46] deduced that there is but one molecular structure present in sufficient abundance to explain the high degree of polarization of all or almost all cell water. It consists of the backbone NH-CO groups of the peptide bonds of proteins in a fully-extended conformation. In the absence of disturbing side-groups (see e.g. gelatin), the backbone of a polypeptide gives an almost perfect fit, sufficient to bridge distances between neighboring proteins in a cell. Ling [12, 18-21] then demonstrated that free NH-CO groups of unfolded proteins are indeed able to bind water strongly, and to orient and polarize it with formation of multilayers. Although extended proteins are essentially linear polymers and not idealized surfaces, Ling argued that there are Ďgenerous margins for effective polarization-orientation of the entire cell water by a relatively small amount of intracellular proteins that assume the fully-extended conformation of an NP-NP-NP systemí [20, p. 127].
Orientation and polarization of water by an unfolded protein matrix are characterized by very low entropy. The question, however, is: from where does the energy to unfold these proteins come? Ling [18-26] found that it came from the stable adsorption of ATP to ATP-binding sites on key proteins, which together with other proteins form an auto-cooperatively linked protein-water-ion ensemble of fully extended proteins, PML-water and adsorbed K+ (see later), which he defined as the cell-matrix. This protein-water-ion complex occurs in cells or parts of cells when they are in the resting (inactive) state (R-state). Relaxed myofibrils are a well-defined example. This state, although low-entropic, is stable in the sense that it can be maintained over long periods without a permanent supply of energy [51, 52], even years in the case of Artemia cysts [52]. However, its low entropy makes clear that it is nevertheless metastable. Its remarkable stability is due to the stable binding (adsorption) of ATP, exerting a strong inductive effect leading to polypeptide unfolding, which is transmitted auto-cooperatively through the whole linked cell-matrix system. Actually the propagated inductive effect has three main effects. It results in protein unfolding, water binding and polarization and K+ adsorption [11, 53]. This concept clarifies the words Ďassociationí and Ďinductioní in the name of this theory: Ďassociation-induction hypothesisí [11, 18-26, 46].
At the moment when Ling introduced his cell-matrix concept [31], the idea of in vivo unfolded proteins would have met with much skepticism. Common perception at the time held that proteins exist in a folded conformation in vivo, mainly because they were isolated as such from living material and continued functioning in vitro. Nowadays, the existence of unfolded or partially unfolded proteins, usually called Ďintrinsically unstructuredí proteins (or IDPs) [54-58], starts to be recognized. According to estimations derived from primary structure data bases 40% of all human proteins contain at least one intrinsically disordered segment of 30 amino acids or more and 25% are likely disordered over their entire length. The other proteins are thought to be globular in vivo [57]. Even if the methods used to arrive at these figures may be far from accurate, the occurrence of both IDPs and globular proteins can no longer be dismissed. These findings shake classical ideas about the relation between a proteinís 3D-structure and its function to its foundations [58]. It should be noted that the ideas associated with IDPs may not exactly correspond to Lingís view of fully extended cell-matrix proteins, but there may be a large overlap. Main difference is that to Lingís view of fully extended proteins a whole basically complete alternative physiology is attached. If explanations for the occurrence of IDPís have to be found, the AIH may give some important answers. Definitely, the modern field of protein biophysics would benefit a lot by taking knowledge of this broad alternative.
Pollack [14] also proposed a very extensive bulk-phase theory: his Ďgel-sol-hypothesisí (GSH). It is built upon the fundamental aspects of Lingís AIH. It takes over most of the concepts of the latter, adds additional evidence for it and explains many physiological processes within this broad context. AIH and GSH are both treated in his very readable book ĎCells, gels and the engines of lifeí [14]. In this book Pollack further explores the cell from the point of view of colloid science. Many details of physiological situations are given whereby controlled unfolding of specific proteins is linked to function and explains the existing data. To the list of cellular processes already described in Lingís AIH (the role of ATP, ion distribution, solute transport, permeability, cell volume control, cell potentials, oxidative phosphorylation, epithelial transport, muscle contraction, control of protein synthesis, growth, differentiation and its malfunction), Pollack adds the processes of exocytosis, amoeboid movement, ciliary beating, mitotic chromosome displacement and cytokinesis. He also remarks that there may be another additional mechanism to obtain multi-layer water orientation and polarization. Some domains of the hydrophilic surfaces of such cytoskeletal proteins as actin and tubulin exhibit a checkerboard pattern of charges at the correct distance (as defined by Ling) to achieve water polarization, even in the folded state. This means that protein unfolding is not always required, although it certainly occurs in many cases.
In Lingís article from 1965 [46] and in certain of his other publications [18, 19, 21], some figures illustrate the orientation of water molecules when bound to an appropriate checkerboard pattern of complementary charges. These figures schematically and in a static way depict the situation in two dimensions. Water, however, has a three-dimensional structure. Chaplin [59, 60] built models to show how polarized water would appear in three dimensions. He described two main conformations of water-clusters, each consisting of 280 strongly bound water molecules operating as if it were a single macromolecule. With this model he could explain almost all properties of water, including the many anomalies. The two conformations were found to be easily transformed into each other without breaking intra- or intermolecular hydrogen bonds. One conformation has high density (HDW, high density water) and is non-polarized; it predominates in normal water. The other conformation has low density (LDW), is polarized and is abundantly present in cells. K+ appears to fit well into the central cavity of LDW, while Na+ does not. The latter ion has a much higher solubility in HDW, in agreement with the observations of Ling [18, 19]. On the basis of this finding, Chaplin proposes a third mechanism for water polarization, whereby K+ ions adsorbed to protein carboxyl groups act as nucleation sites for the formation of an LDW cluster with high polarization, from which water polarization spreads further.
This idea agrees with the extensive studies of Wiggins [61] on the properties of HDW and LDW. She showed that both types of water can be obtained in the small pores (averaging 2 nm diameter) present in cellulose acetate films. Certain ions (K+, NH4+, Cl-, HCO3-, HSO4-, H2PO4-) appear to fit well into the central cavity of a LDW cluster and exhibit reasonable solubility. Others (H+, Li+, Na+, Ca2+, Mg2+) do not fit, but fit and show good solubility in HDW. Surprisingly, it was also found that at high concentrations the first group induces the conversion of LDW into HDW, while the second group at high concentrations induces the conversion of HDW into LDW. These properties make it possible to generate a cycle. In a remarkable experiment, Wiggins and MacClement [62] succeeded in synthesizing ATP from ADP and KH2PO4 (5 mM) in the presence of 100 mM KCl, with the pores of cellulose acetate forming the micro-domains of water and with no additional energy input. A major difference from the enzyme-catalyzed reaction is that it requires a few days, but one can learn from the mechanism. It is quite possible that hydrolytic and biosynthetic enzymes, including ATPases and ATP synthase, evolved as catalysts of this older HDW-LDW cycle. Proposals are given as to how the two states of water may contribute to the mechanisms of cation pumps and other enzymes. This is a real opportunity for the study of these enzymes, including Na+/K+-ATPase.
The three mechanisms for water polarization (Ling, Pollack and Chaplin) do not exclude each other. Their relative contributions, however, remain to be determined. These three mechanisms and the more general idea of water orientation and polarization are also in full agreement with Kaivarainenís new fundamental physical theory of phases, called Ďnew hierarchical physical theory for the solid and liquid phasesí, which is derived from basic principles [63]. Kaivarainen gives many applications of his theory to cell biology.
4. The Adsorbed State of Cellular K+
After the experiment of Hill [2, 3] had set the stage in favor of MT, some other experiments seemed to prove that cellular K+ is free. However, it was demonstrated later that these experiments or their interpretations were also problematic [12, 18, 19, 22, 64]. In contrast, a large number of different approaches all point to bound K+. Some of these studies do not allow us to decide where and on which kind of binding sites adsorption occurs. Others, however, give this information quite specifically.
Indications for bound K+ as such comprise: (a) the study of distribution coefficients by Ling et al. [32] discussed above, indicating that Hill [2, 3] found an exception by only studying urea; (b) the fact that resting muscle cells without an intact cell membrane (EMOC preparations: see further) are able to sustain normal intracellular K+ concentrations for at least two days [51]; (c) the demonstration that Artemia cysts survive for four years without energy consumption [52]; (d) reinvestigations of measurements of ionic conductivity in various cell types and of K+ mobility in frog muscle cells, giving much lower values than for free K+ and providing convincing explanations why some earlier studies gave high values [12, 18, 19, 22]; (e) proof that use of a K+ selective electrode readily injures the cell, resulting in much too high activity measurements, so that more confidence can be given to those experimental setups giving low values [18, 19, 22, 64]; (f) X-ray absorption-edge fine structure determination of red blood cells giving a result that differs markedly from control measurements on a KCl solution of the same concentration [65]; (g) 39K+ NMR spectra of neurons, muscle cells and E. coli, which produced relaxation times much shorter than those of 0.1 M to 0.4 M KCl solutions and comparable to those of K+ adsorbed on a Dowex-50 cation-exchange resin [66, 67, 12, 18, 19, 22]; (h) demonstration that the relationship between internal and external 42K+ concentration follows Langmuirís adsorption isotherm, whereby real proof of adsorption was given by studying the influence of inhibitors that compete in different ways for the same adsorption sites (unlabeled Cs+ and unlabeled K+) [19, 68].
In 1952, Ling had already deduced that K+ might be adsorbed to the β- and γ-carboxyl groups of proteins [11, 12, 18, 19, 22]. Kellermayer et al., [69] showed that K+ remained associated with cytoskeletal proteins for several minutes after treatment of living cells with the non-ionic detergent Brij 68, whereas if it were freely soluble in the cytosol its liberation would have been detected in seconds. In addition, a stoichiometric relationship between protein carboxyl group concentration and K+ concentration was demonstrated [19]. The most convincing results, however, came from the extensive electron microscopic investigations of frog Sartorius muscles mainly by Edelmann [70-72], using most delicate preparation techniques and advanced methods of analysis. Freeze-dried embedded and frozen hydrated thick sections of chemically unfixed specimens were used without staining, so that the location of K+ (by far the most abundant metal) could be directly observed. Alternatively, specimens in which K+ was partially substituted by one its more electron dense competitors, Rb+, Cs+ or Tl+, were used. In all cases K+ or its analogue was preferentially located in the A-band, where the heads of myosin are exclusively present, with a fainter electron density at the Z-line. Quantification was obtained with electron probe X-ray microanalysis (see also [73]) and laser microprobe mass-spectroscopic analysis. Autoradiography of single air-dried [19] or frozen fully hydrated muscle fibers [72] using 86Rb and 134Cs revealed the same specific localization.
The presence in the cell of PML-water and adsorbed K+, for which abundant arguments have been given in this and the foregoing sections, are a necessary condition for reaching coherence. Coherence needs nearest neighbor interactions of the correct extent. The law of Nernst, as applied by MT, is based on the independence of solute molecules, i.e. the absence of interactions, so that stochastic behavior ensues. Arguments for coherent cellular behavior, which are the subject of the next section, are in fact supplementary arguments for a high level of order, also with respect to water and the main cation, K+.
5. The Coherent Behavior of Life
In his book ĎWhat is life?í Schrödinger [17] argued that concentrations of many important cellular components are too low to apply statistical laws in a meaningful way. This is the case for DNA and some regulatory substances and even for ions in small cells and subcellular compartments. In particular, Schrödinger envisioned the laws of diffusion, which are also part of the law of Nernst. To give an example: in liver cells an average mitochondrial matrix at neutral pH contains six free protons during state IV and only one during state III (fully activated and contracted). How one can make a bulk gradient with that [74]? In order to alleviate this undeniable difficulty, Schrödinger proposed that cellular processes may make use of coherent mechanisms, analogous to those found in physical systems close to absolute zero but applicable at body temperature. His argument was that such mechanisms are much more precise and able to operate below the level of thermal noise, exactly what would be needed to explain life. His proposal was largely neglected, mainly because at that time all data, in particular the findings of Hill [2, 3], were pointing towards the laws of diffusion and of Nernst as providing exact explanations for cell physiology. As a result, investigations into lifeís coherence originated at the very margins of biological science. Several independent approaches to the question of the coherence of life will be reviewed.
1 Ling's AIH [11, 53] was probably the first broad physiological theory in which coherence figured as a central theme: actually as the primary mechanism of all actions in living cells. In the R-state the cell-matrix is seen as a metastable high-energy low-entropy polarized coherent whole, a cooperatively-linked protein-water-ion complex. It is a coherent static system extremely sensitive to all kinds of very weak stimuli. When the energy delivered by a stimulus and mediated by Ca2+ (or another mediator) reaches the activation threshold, the system as a whole undergoes a conformational change, leading to the A-state, which is less polarized and has lower energy and higher entropy. The energy difference between the R- and A-states, attributable to an increase in entropy, is used for biological work: mechanical, electrical, chemical, transport work and coherent emissions (see later). The higher entropy is due to folding of the cell-matrix proteins, whereby adsorbed layers of water are depolarized and dissociated together with K+. This is just what Schrödinger imagined: life processes energized by negative entropy.
The conformational change itself is also a coherent process, but of a dynamic type. This can be understood from the all-or-none character of the folding of a random coil into an α-helix (or other type of protein secondary structure), and, linked to it, the all-or-none character of long-range water depolarization. Biological work is performed at the onset of this conformational change, because the suddenly-formed secondary structures bring about interactions with other activated molecules, in which interaction-capable secondary structures appear as well (see also [15]). The formation of actomyosin is a good example. At the end of this dynamic process, after work is done, the cell-matrix ends up in the A-state, which is much less coherent; perhaps even not far from an irreversible death state. In muscle cells the A-state is called rigor mortis. In a healthy living cell, however, metabolism synthesizes new ATP, which binds to the ATP-binding proteins of the cell-matrix and restores the high-energy low-entropy R-state. Proteins again unfold, re-adsorb and polarize cell water, and re-adsorb K+. Metabolism thus brings about the reverse conformational changes, also a dynamic coherent process. Metabolism is the factor that prevents the death state from succeeding the A-state. It is responsible for reversion to the R-state following power output. This R-to-A-to-R cycle and its energetics was already developed by Ling in his first book (1962, [11]). It is presented graphically by the red line in Fig. (1) (the green line will be explained at the end of this article).
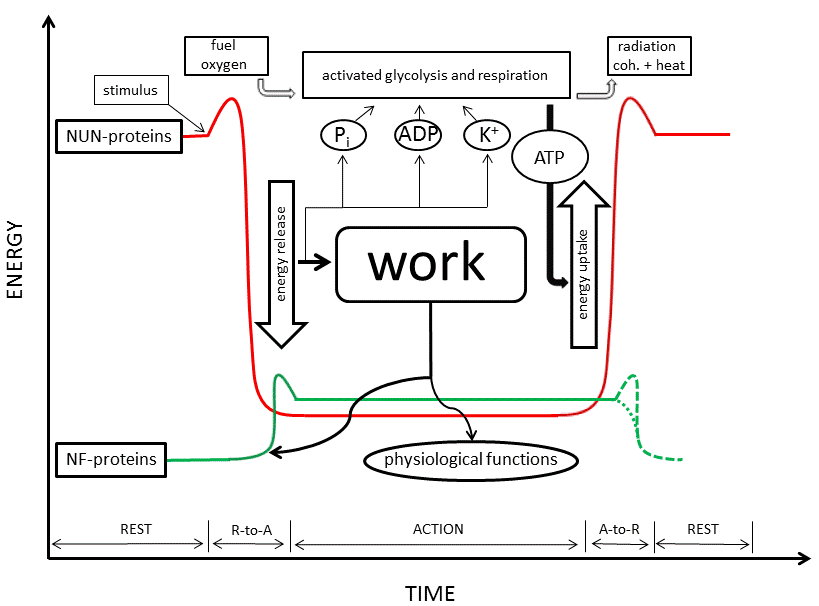
Fig. (1). Energy levels of natively unfolded proteins (NUN) (red line) and natively folded proteins (NF) (green line) in the resting-state (R), action-state (A) and during R-to-A and A-to-R phase transitions. The energy level of NUN-proteins relative to that of NF-proteins during the A-state is approximately. For both groups it is somewhere between the levels of the fully unfolded state (see: NUN-proteins during the R-state) and fully folded state (see: NF-proteins during the R-state). The exact values depend on the kind of protein, but the energy difference of the R-to-A transition is always greater for NUN-proteins than for NF-proteins. During the R-state, NUN-proteins are inactive. They are unfolded, polarize cell water and adsorb K+, creating a high-energy low-entropy metastable state. A sufficiently strong stimulus is needed for them to leave their high-energy basin (threshold). NF-proteins are inactive as well during the R-state because they are tightly folded, hiding their reactive centers inside. Slight melting to an intermediate state is needed to expose these centers and make them active. The frame representing glycolysis and respiration points towards the processes that convert fuel, oxygen, ADP and Pi into CO2 , H2O, ATP and radiation (both coherent and waste heat), but is not intended to lie on the energy axis. Energy of entropic origin released during the R-to-A transition of NUN- proteins is used for activation of NF-proteins and for biological work (physiological functions). K+, Pi and ADP liberated during the R-to-A transition of NUN-proteins is thought to activate major rate controlling enzymes of glycolysis and respiration, in agreement with known allosteric mechanisms. So formed new ATP adsorbs to NUN-proteins and causes their A-to-R transition. Subsequent lowering of K+ and ATP activity deactivates glycolysis and respiration. A-to-R deactivation of NF-proteins either needs a small amount of energy to leave their A-state high-energy basin or is a spontaneous process, probably depending on the case. Therefore, both possibilities are drawn with dotted lines.
Small note: according to Ling [18], liberation of rather large amounts of K+ in local myosin-containing compartments of muscle cells brings about strong local unidirectional osmotic fluxes of water towards that region, and this is the major force that brings about contraction, a mechanism that explains the concomitant thickening of muscles. Apart from this interesting proposal, a very penetrating controversy exists with respect to the energetics of muscle contraction. Formation of firm protein-protein (actin-myosin) linkages, when considered on its own, may at first sight imply a decrease in entropy. If the assumptions of MT were correct Ė i.e. if the physical state of cellular water and K+ during the R- and A-states remained the same - the classical conclusion that muscle contraction is a Ďdisorder-to-order transitioní [75] appears logical. But all the evidence favors Lingís alternative view, with desorption and depolarization of water and desorption of K+ during the R-to-A transition. It then follows that the small decrease in entropy due to actomyosin formation is largely offset by the large increase in entropy due to liberation and depolarization of water and K+ desorption. Therefore, exactly the opposite is true: muscle contraction is an Ďorder-to-disorder transitioní. The release of rigor by addition of ATP [76] is the ultimate corroboration of Lingís and Schrödingerís view. The survival of Artemia cysts for long periods, with measured zero-energy consumption [52], is also consonant with this. The above controversy illustrates the problem with MT not involving a holistic physical approach to the study of life, and underlines the need of a new model for cell energetics.
According to Ling [11, 12, 18, 23, 24, 53] the mechanism that brings about the R-to-A and A-to-R conformational changes is based on the induction effect of Lewis: the basis of chemistry, hence also of biochemistry. This mechanism includes the inductive effects exerted by so-called Ďcardinal adsorbentsí at the site of induction and their long-range propagation and spreading throughout the cooperatively-linked proteins of the cell-matrix. Cardinal adsorbents are controlling substances binding to controlling binding sites (cardinal adsorption sites) on the cell-matrix. They include: all kinds of external and internal stimuli, hormones, neural transmitters, growth factors, second messengers, nucleotides and other allosteric modulators, drugs, etc.. For instance, in the case of myofibrils, Ca2+ is the activator and ATP restores the R-state. The sites for binding water, K+, etc., are called Ďregular adsorption sitesí, while the binding sites for ATP or Ca2+ are cardinal adsorption sites, because of their controlling function and their one-on-many effect. Indeed, the inductive (electron withdrawing) effect of the binding of one ATP molecule to one corresponding ATP binding cardinal adsorption site is propagated and spread through the whole system of auto-cooperatively interconnected proteins, reaching not only all these proteins but also all associated PML-water and all adsorbed K+. Temporary chemical modifications of proteins such as phosphorylation can play a similar role to cardinal adsorbents.
The essential feature of cooperativity, in contrast to non-cooperativity, is energetic interaction between near-neighbor sites. It is described quantitatively in the theoretically-derived ĎYang and Ling cooperative adsorption isothermí [11, 14, 18, 19, 23, 24, 53]. This equation allows of auto-, hetero- and non-cooperative adsorption phenomena to be precisely verified experimentally, and has been applied as such by Lingís group to many of their own experiments as well as to many existing data in the literature. It is analogous to (but more general than) the empirical equation developed by Hill describing the oxyhemoglobin dissociation curve. Ling also showed that the polypeptide backbone possesses the unique property of high polarizability and partial resonance, allowing it to act as a high-way for the propagation of inductive effects, resulting in water adsorption and polarization or desorption and depolarization. Propagated inductive effects also reach side chains resulting in K+ adsorption or desorption from β- and γ-carboxyl-groups and some comparable effects on positively charged side groups. On the basis of the inductive effects, all cardinal adsorbents were divided into two groups (eventually three): those generating an electron-withdrawing inductive effect (e.g. ATP) and those generating an electron-donating inductive effect (e.g. Ca2+). The third possibility, an electron-neutral effect, is probably not very relevant to functional processes.
2 In the late 1960s, Fröhlich [77, 78], a pioneer of the study of coherent behavior in physical systems near absolute zero, started exploring the eventuality of coherent behavior in living systems at physiological temperature. As a physicist he approached the problem from a completely different point of view, namely from electrodynamics. Living organisms are mostly made of dipolar (dielectric) molecules in a phase system, which is a quasi solid state. This implies that electric and visco-elastic (mechanical) forces may be in permanent interaction. The function of metabolism is to Ďpumpí the living system into an excited state. It should be noted that the latter idea is consistent with Lingís R-state. Fröhlich uses the word Ďpumpí in a way that differs from its meaning in MT, because the excited state obtained by this pumping can be metastable. He uses pumping in the way Ling sees the function of ATP in restoring the high-energy R-state. The ensuing excited state is characterized by collective modes of vibration of a coherent nature. This holds that the giant dipolar structures of proteins, nucleic acids and some larger ensembles such as membranes, with their enormous electric fields (107 V/m), start to vibrate at characteristic frequencies common to the different components belonging to the system. These collective oscillations originate through the coupling of electric dipole displacements and mechanical displacements. Resonances may lead to emission of both electromechanical oscillations (phonons or sound waves) and electromagnetic radiations (photons), which may exhibit coherence as in a laser. These are propagated over a rather long distance, so they can eventually be measured outside the organism. This is the way to obtain information about the existence of these coherent collective modes. Alternatively, organisms can be subjected to extremely low intensities of the appropriate frequency, and this will lead to excitation of the corresponding cell function by resonance. Both approaches to these so-called Ďcoherent excitationsí have been experimentally tested with positive results [79-82].
The group of Cosic [83, 84] further elaborated this idea in their ĎResonance Recognition Modelí. They used a calculation to transform an amino acid sequence into a frequency pattern. When this was done for proteins exerting similar functions, a typical common frequency was always found, indicative of that function, but also found in the frequency spectrum of their targets. It follows that it is characteristic of their reciprocal attraction and recognition by resonance. The frequency range for protein interactions is 1013 to 1015 Hz (equivalent to the near-infrared, visible and near-UV spectra). Common frequencies were calculated and also measured, and the measurements were found to match the calculations. The authors concluded that the specificity of protein interactions is based on resonant electromagnetic energy transfer at a frequency specific for each kind of interaction or function.
Fröhlich described three kinds of coherent excitations [80-82]. The first is static (metastable), low-entropic and highly polarized and became known as the ĎFröhlich stateí. Jaeken [85] argued that the R-state as described in physiological and molecular detail by Ling and Pollack (gel-state) conforms to the more general physical description of a Fröhlich state, formulated in terms of frequencies. Both descriptions evoke a low entropy, metastable (static), highly polarized, long-range coherent, excited (high-energy) state obtained through input of metabolic energy (ATP). The Fröhlich state is characterized by condensation of all modes into a single frequency, exhibiting coherence. Clearly this is due to the auto-cooperative linkage between all parts in Lingís description. Second, Fröhlich also described a dynamic type of coherence, called a ĎFröhlich waveí. The R-to-A (gel-sol) and A-to-R (sol-gel) phase transitions described in physiological and molecular terms respectively by Ling and by Pollack were both shown to conform [85] in physical terms to a Fröhlich wave. Third, Fröhlich envisioned the existence of coherent cyclic processes, known as Ďlimit cyclesí [80-82, 85, 86]. The rhythmic succession of action states occurring for instance during prolonged muscle activity Ė if understood according to Lingís AIH or Pollackís GSH (but not according to MT) - exemplifies such limit cycles [85].
3 In the early 1970s a third independent approach was taken by Davydov [87-90, also 91 for review]. He applied quantum mechanics to protein á-helices and showed theoretically that the latter might be able to conduct non-dispersed one-dimensional elastic lattice pulses along their length, which became known as ĎDavydov-solitonsí. The concept of Ďsolitonsí is used in non-linear physics to describe the loss-less transmission of waves of any kind. In the case of Davydov-solitons, dispersion of mechanical pulses along an α-helix (in an apolar environment) is exactly counteracted electronically by enhanced inductive effects on the longitudinal amide-2 hydrogen bonds, so that coherence is reached. Similarly, Davydov also described Ďelectro-solitonsí and Ďprotonic solitonsí (loss-less displacement of an electron charge respectively a protonic charge along an α-helix) [89] (see [91] for an overview). One or more of these types of solitons are believed to travel along microfilaments and microtubules, providing them with the ability to transmit and process data [92, 93]. Indications for this were recently supported by direct evidence [94]. A much more complex type of soliton is the action potential [91, 95], a well-studied example of a rest-to-action-to-rest (R-to-A-to-R) (gel-sol-gel) double phase transition [14, 18, 19, 36, 39, 95] in agreement with Lingís AIH, Pollackís GSH and the Fröhlich wave concept [80-82]. These studies show that an action potential is much more than the outdated concept of temporary permeability change MT proponents believe (see Ling [12, 18, 19, 36]).
4 The group of Del Giudice [86, 96-99] followed a fourth path, starting from quantum field dynamics. The phenomenon, which in their theory is described as a ĎBose condensationí and its reverse, here called ĎBose decondensationí, was shown to correspond to the description of Fröhlich waves [80-82, 86, 96,] and to R-to-A (gel-sol) and A-to-R (sol-gel) phase transitions according to AIH and GSH [85]. Actually, the four independent approaches described above could all be unified using Lingís physiological paradigm as a basis [85]. This unification was achieved by interpreting the four coherent solutions of a non-linear Schrödinger equation, derived by Tuszinsky et al., [100], who had already united the views of Fröhlich and Davydov.
5 A fifth independent approach came from quantum non-linear optics [101-106]. Using specifically developed optic instrumentation, Popp [101] obtained quantitative measurements of the extremely weak photon emission (not to be confused with bioluminescence) of all living organisms in the visible and UV region, first observed by Gurwitsch and Gurwitsch in 1922 [102]. He proved the coherent (laser) properties of these so-called Ďbiophotonsí, defined as coherent photons produced by living organisms [103, 104] but absent at death. Biophotons may be produced by DNA [98, 103-106] and by micro-tubules, whereby excited water plays a particular role [98, 99, 106]. Their coherent nature allows holograms to be generated, with all the remarkable properties of the latter including distributedness and extremely high information density, and offering the possibility of constructive (within cells) and destructive (between cells) interference [92, 104]. Popp proposes that biophotons are ideally suited to coordinating the behavior of otherwise independent molecules located at distant places in cells, tissues, organs and even the whole body; and they could do this at the speed of light. Popp [88] concluded in a general way: Ďbiophotons may well provide the necessary activation energy for triggering all biochemical reactions in a cell at the right time at the right placeí. In that respect, they are responsible for the common observation that a body acts as a single unit, despite it being composed of innumerable individual molecules. Precisely this unity of behavior constitutes the problem with which Schrödinger struggled. Of course, the coherent nature of biophotons would be dispersed if they had to trave through a non-coherent cytoplasm, as assumed by MT.
6 Ingber [107, 108] demonstrated the tensegrity properties of the cytoskeleton. The latter consists of a three-dimensional construction of compression-resisting struts (microtubules) interconnected in an indirect way by means of pre-stressed microfilaments and intermediary filaments, which have more elastic properties, or which by sliding past each other acquire properties equivalent to elasticity. In mechanics such systems are called 'tensegrity structuresí. They exhibit tensegrity properties, which means that they behave as a unified whole in response to external mechanical forces, which become distributed over the entire network and result in global rearrangements. In this way a cell also achieves mechanical coherence [109]. The observed pre-stress [107] means that the cytoskeleton Ė also when at rest Ė stores mechanical energy and hence the R-state is also a high-energy structure from the mechanical perspective, complementing Lingís view. This property makes it very sensitive to weak mechanical influences. Because cells are connected by integrins and junctional complexes to neighboring cells and to extracellular matrices, which also exhibit tensegrity properties, entire tissues and even organs exhibit tensegrity. The tensegrity concept allows us to explain how mechanical stimuli influence cellular information processing in the cytoplasm and in the nucleus through connections with the nuclear skeleton [108]. Some of its effects at the transcriptional level participate in morphogenesis, both normal and anomalous as in the case of cancer [108]. Because both the cytoskeleton and the extracellular matrix (i.e. collagen) exhibit piezoelectric properties [110], mechanical coherence goes along with electrical coherence [109]. And because many proteins, multi-protein systems and cell organelles are connected to the cytoskeleton [111] and can be directly influenced by data processing along the cytoskeletal network [92-94], chemical coherence may also become aligned with both mechanical and electrical coherence [109].
7 Finally, Ho [49], pursuing the idea that coherence ought to be reflected in its structural organization down to the atomic and molecular level, went to the polarizing microscope and indeed directly observed the structural coherence of entire living cells, even organs in living organisms, proving that Schrödingerís early proposal was fully justified. Ho [49] and Abbott [112] reviewed the indications that living organisms are indeed quantum coherent and can be regarded as macroscopic quantum systems. Recently, the existence of quantum coherence was directly measured in several in vitro experiments on parts of the photosynthetic apparatus [113-116].
In view of all these lines of evidence, direct and indirect, and the strong theoretical foundations from so many different independent approaches, which all point in the same direction, the coherent behavior of life can no longer be dismissed. Moreover, applications are quickly being made, particularly in diagnostic and therapeutic medicine, as there are increasingly strong indications that the lack of a sufficient level of coherence is the primary cause of cancer [117]. Genetic defects appear to originate later and secondarily as a result of insufficient coherence, which in a non-specific and progressive way destabilizes molecular and gene regulatory networks [117]. Despite all this evidence for coherence, together with the evidence for adsorption and polarization of water and adsorption of K+ to cell-matrix proteins , there is a major persistent obstruction to the uptake of these data by general textbooks and university courses. This obstruction is the persistence of MT. Therefore some additional evidence against an important aspect of MT, the concept of the Na+/K+ pump, must properly be given.
6. Evidence Against the Concept of Pumps
The lines of evidence discussed below are not against the existence of Na+/K+-ATPase, nor against the main steps of its working mechanism as it is understood at present [27], but against the way of thinking about this enzyme/transporter as the pump responsible for the steady state concentrations of Na+ and K+ in cytosol.
Evidence against the pump hypothesis properly includes the following.
(1) Full inhibition of respiration and glycolysis in cells kept at 0įC, blocking the energy supply to the Na+-pump, did not result in a reduction of Na+ efflux. This early experiment of Ling [11, see also: 12, 18, 19, 22, 25] was later confirmed with cells at 17-23įC by Keynes and Maisel [118] - although Keynes later adopted MT - and by Conway et al. [119]. Extensive controls for remnant energy sources (creatine phosphate, ATP, ADP, lactate) and heat output measurements were undertaken (discussed by Ling [11, 12, 18, 19, 25]), confirming that the observed Na+ efflux was independent of a continuous energy supply. All authors agreed on the data. Taking the measured Na+ efflux rate, a resting potential of -90 mV and the method of calculation customary in MT, the conclusion Ė quoting Ling [11, 12, 18, 19, 25] Ė was: Ďthe minimum energy needed by the Na pump at the plasma membrane alone was from 1542% to 3050% of the maximum available energyí. Comparable work done by Minkoff and Damadian [120] on E. coli led to a similar conclusion.
(2) The general consensus [27] is that in neurons, without inhibition of metabolism, the Na+/K+ pump consumes about 60% of the cellís energy. However, there are many more pumps and they are located not only in plasma membrane, but also in the much larger area of intracellular membranes. Energy is also needed for cytoskeletal movement, for anabolism, regulation, etc. So, energy shortage remains a problem. If one considers that the R-state of a cell in the AIH perspective is a (metastable) physical equilibrium not consuming energy (see point 4 below for experimental proof), the problem of energy shortage is entirely taken away.
(3) Investigators in several laboratories (summarized in [12, 18, 19, 25]) observed Na+ exclusion and K+ accumulation in red cell ghost preparations upon addition of ATP, but only when these were prepared according to the method of Bodemann-Passow, which yields ghosts that are not pure membrane but are filled with cell-matrix (mainly hemoglobin, some actin and minor components). In contrast, when cytoplasm-free red cell ghosts consisting of pure membrane are prepared using methods with more thorough washings (discussed in [12, 18, 19, 25]), pumping activity was never observed. Obviously, this indicates that something in the cytoplasm is necessary for establishing ATP-dependent gradients [11, 12, 18, 19, 23-26].
(4) In 1978 Ling [51] conducted a long series of experiments with so-called ĎEMOC preparationsí (EMOC = effectively membrane-(pump)-less open-ended muscle cells). Isolated resting frog Sartorius muscles were cut in the transverse direction and the membrane-less open-ended part was inserted into a Ringer solution, while the upper closed and membrane-delineated part was kept in the air. At the open-ended part in contact with the Ringer there are no membrane-bound pumps because there is no membrane, while in the upper part pumps present in the membrane cannot work because they are not in contact with the external Ringer solution (this was controlled). The intracellular concentrations of Na+ and K+ in the upper part of the cell remained unchanged for at least two days, despite the huge leak at the open end. Radioactively labeled 40K+ in the Ringer revealed that during this long period there was indeed transport of the label from the Ringer into the upper part of the cells, proving the existence of a K+ influx in the absence of effective pumps. The conclusions are surprising but straightforward. Since pumps must be ineffective in these EMOC-preparations, the constancy of the total concentrations of Na+ and K+ in the upper part of the cell over two or more days cannot be due to a steady state, as MT proposes. There is only one alternative: they must be due to a true physical equilibrium. This also means that neither pumps nor an intact membrane are necessary to maintain this situation. Classical cell energetics clearly needs to be replaced by a completely different mechanism consistent with these observations (or at least using this possibility as an additional control for experiments on "membraneĒ transport).
From previous sections, a sound explanation of the EMOC experiments as conducted by Ling can be readily inferred. According to Ling, the intracellular Na+ concentration remains low despite direct open contact with a high Na+ concentration Ringer because Na+ is very poorly soluble in intracellular water that is polarized by the cytoplasmic colloid (interconnected cell-matrix); and the intracellular high K+ concentration remains high despite open contact with a low K+ concentration Ringer because K+ is largely adsorbed to the β- and γ-carboxyl-groups of the proteins of the same cytoplasmic colloid. He gathered substantial evidence for these two proposals (see earlier) [11, 12, 18-26, 51]. Together, these two effects (adsorbed water and K+) generate a physical equilibrium that has no need of a special membrane or of ion pumps located in it. Of course, an intact cell has a plasma membrane and hence these ions must pass through this membrane, but the function of proteins such as Na+/K+-ATPase must be different from that assumed by MT (see later). These EMOC experiments seem impossible to reconcile with a steady state theory and explain why the problems described above under points 1 to 4 exist. Instead of applying the Nernst equation to the total ion concentrations, as MT does, Ling [11, 12, 18, 19, 25] developed a new set of formulae in which distribution coefficients, diffusion effects and adsorption coefficients figure and total concentration is distinguished from activity (the free fraction). In contrast, MT does not even have a formula describing observed concentrations and is often careless about the concepts of concentration and activity (instead of explaining their physical nature).
(5) When authors (without exception) tried to prove the pumping function of Na+/K+-ATPase experimentally they were biased by the belief that this is the real function of this enzyme. It was like asking the Pope to prove the existence of God. Sorption processes were not considered as a real alternative to the ion-pump in any study devoted to the transport function of Na+/K+-ATPase (see [45] for review). Nevertheless, there has been abundant direct evidence for a bound state of K+ in living cells at least since the early 1980s (see [70] for review).
(6) It is always necessary to get important evidence from the opposite approach: namely, proofs indicating that all other explanations can be dismissed (as Ling does for MT). However, a large number of experiments together with a firm theoretical background point towards a serious alternative explanation for the actual Na+ and K+ distributions, which to date has remained effectively unchallenged. Each challenge was followed by a rebuttal [20-26].
(7) Using EMOC preparations Ling [12, 18, 19, 25] made another crucial observation. In older EMOC preparations the cell-matrix at the open end gradually started to degrade. In the degraded parts, the Na+ concentration was higher and the K+ concentration lower than the normal cellular concentrations found in the non-degraded parts further away from the open end. Ling was able to observe a good correlation between local ion concentrations and local ATP concentration. It was found that a minimal ATP concentration is needed to keep water sufficiently polarized to maintain a low Na+ concentration and to keep K+ sufficiently adsorbed to maintain a high K+ concentration [12, 18, 19]. This relationship was beautifully addressed by Kellermayerís group [121-123]. Red blood cells have a very narrowly-defined function. This probably explains why intracellular erythrocyte Na+ and K+ concentrations vary widely among different species and even within members of the same species, although the concentrations of these ions in the blood are very similar. In human red blood cells, Na+ and K+ concentrations are normal as in other cells. But dog erythrocytes contain 10 times more Na+ than K+. If MT is correct, the cause of this aberration has to be found in the working of the Na+/K+ pump. If AIH is correct, the cause should be an abnormally low ATP concentration. Although a relatively good correlation exists between the activity and/or the amount of Na+/K+-ATPase and the steady state levels of Na+ and K+ [122], the uptake rate of Rb+ (a widely used K+ analogue) is much higher than its leakage rate, irrespective of the kind of red blood cells [123]. This compromises any tight coupling between pump activity and leakage rate and therefore the whole steady state idea. In contrast, in the different kinds of red blood cells studied, there is a clear relationship between ATP concentration, Na+ and K+ content and the intracellular K+/Na+ concentration ratio. All this makes it clear that ATP is the crucial factor for maintaining the physical equilibrium, but as the experiments under points (1) and (7) demonstrate, ATP does not need to turn over by means of hydrolysis in order to keep the ion concentrations constant. Thus, the manner in which ATP energizes cellular systems has to be re-addressed, though MT has kept Lipmannís idea of Ďhydrolysis of ATPís high-energy bondí on the stage for more than 70 years.
7. The Mechanism of Energy Delivery by ATP
A central topic associated with the working of the Na+/K+ pump is how ATP energizes this system and other systems as well. The view offered by MT differs in a most fundamental way from that of Ling in his AIH. According to MT, energy is derived from the hydrolysis of ATP. MT followed the idea of Lipmann [8] that the phosphate-anhydride bond of ATP is a high-energy bond able to inject its binding energy into the system at the moment of hydrolysis. This would mean that the initial stages of strong actin-myosin binding constitute a higher energy state than dissociated actin and myosin in the relaxed state (see: the discussion on muscle contraction given before [75]). This is exactly opposite to the view of Ling [12, 18-26, 51]. According to Lingís AIH, two properties of ATP are responsible for its mechanism as an energizer of cellular processes: (1) it can bind to cardinal binding sites on some proteins of the cell-matrix, whereby the adsorption energy lifts the system into a metastable high-energy low-entropy R-state (the R-state is high-energetic); (2) it can also be eliminated from these binding sites by the ATPase activity of these proteins. The latter property is important for the R-to-A transition involved in power output.
Concerning the first property, the free energy of adsorption is huge: -39.7 kJ/mole for adsorption on (A-state) actomyosin [124] and -46.0 kJ/mol for adsorption on G-actin [125]. The equilibrium on G-actin adsorption constant in the case of (A-state) actomyosin is 9.84x106 [126], meaning that only 1 ATP molecule out of 9.84 million remains free. This also means that ATP does not have the opportunity to travel a long distance in the in vivo situation of macromolecular crowding. ATP generating enzymes must therefore be located in close vicinity to systems utilizing it. The role of ATP adsorption in restoring the R-state is well-established, most obviously in the case of unlocking rigor of actomyosin [76]. The stability of the resulting ATP-cell-matrix ensemble was proved by the experiments of Ling on EMOC preparations [51] and those of Clegg [52] on Artemia cysts. However, some discussion may remain about the exact moment of enzyme-bound ATP hydrolysis: before or after initiation of the R-to-A transition.
Concerning the second property of ATP, most proteins that can adsorb ATP also possess ATPase activity. But the moment of hydrolysis may not be regarded as Ďtheí energy injection. First of all, this would neglect the high adsorption energies mentioned above. Secondly, enzyme-bound ATP hydrolysis is often close to equilibrium [127, 128]. In classic views the latter observations are not denied, but lead to possibly unrecognized confusion (see the controversy above about actomyosin formation, which is sometimes regarded as a mysterious ĎMaxwellís demoní [129]); a consequence of not having a holistic approach to cell physiology and of having ignored Lingís AIH for so many years. Adsorption constants for ADP and Pi are much lower than for ATP. This allows ADP and Pi to dissociate, which is actually exergonic. So, energy stored in the high-energy low-entropy R-state can be tapped and transformed into work during the R-to-A transition in a stepwise manner and concomitantly with Pi and ADP liberation. Lingís mechanism for ATP, which is intimately linked to the high-energy low-entropy status of the R-state, corroborates and adds detail to Schrödingerís idea: ĎLife feeds on negative entropyí.
After the above discussion of the properties of ATP, current models of the Na+/K+-ATPase are surrounded with questions. Why is nothing said about the adsorption energy of ATP? It is likely that the high energy state is achieved at the moment of ATP binding and not during the next step, when a phosphate group is transferred from ATP to an aspartate residue on the protein. How the reaction step, not really a hydrolysis but a transferase activity, could be an Ďenergy injectioní? Why are the effects of structured water at the membrane surface not taken into account? Given the data of Wiggins [61, 62] on ATP synthesis by means of changing the water structure, and given the idea that changes of water structure are likely to produce large differences in free energy on entropic grounds, this question should elicit immediate experimental verification. Why is it not seen that changes in binding preferences (affinities) for one kind of bound ion in favor of another (for instance Na+ instead of K+ or the reverse) is a quantitatively well described process in terms in Lingís AIH, which states that these (observed) affinity changes are brought about by inductive effects exerted by cardinal adsorbents? The two affinity changes that occur during the transport cycle of the enzyme could be explained by changes from an electron withdrawing effect to an electron donating effect; and this has already been demonstrated. Indeed, under experimental conditions, Na+/K+ ATPase can be made to synthesize ATP. It is usually said that a sufficiently large gradient of Na+ and K+ is required to achieve this. However, Post et al. [130] succeeded in synthesizing ATP with a purified protein without an ion gradient. They concluded that Ďbinding of sodium ion to a low-affinity site on the phosphoenzyme formed from inorganic phosphate is sufficient to induce a conformational change in the active center which permits transfer of the phosphate group to adenosine diphosphateí [130]. The step of phosphorylation of the enzyme by Pi requires the presence of Mg2+ and K+, while the subsequent step of ATP synthesis from ADP and the phosphoenzyme is inhibited by Mg2+ and stimulated by Na+. By just reversing causes and effects one obtains the process in the ATPase direction. These findings, although they were not inspired by the AIH, completely shift attention from MT (based on ionic gradients) to the AIH (based on adsorption and its inductive effects) [18].
Why are the properties of ATP in a colloid environment not taken into account? ATP is highly soluble in ordinary water, as every biochemist discovers when he prepares an assay mixture. But oddly enough, the broader physical properties of ATP, which determine its behavior in colloidal Ďsystemsí, are recognized by neither chemists nor biologists. No one knows how ATP is distributed among the components of some commonly-used colloidal systems (cells, cell ghosts, vesicles reconstituted from purified Na+/K+-ATPase). All that is known at present is that ATP is amphipatic: log P = 1.64, where P is the partition coefficient of ATP in an octanol/water system [131] (for comparison, hexanol log P = 1.46 [131]). ATPís amphipaticity indicates that it does not just swim in a solution, but must be distributed among the components of any colloidal system according to local hydrophilic respectively hydrophobic properties. Cells, cell ghosts and reconstituted vesicles with built-in-Na+/K+-ATPase all contain lipids and enzyme molecules that also have hydrophobic domains (see [132] for review). Since it is not known how the amphipaticity of ATP affects the properties of the colloidal systems studied, the data in favor of the pumping function of Na+/K+-ATPase cannot be considered as proof; nor can those on reconstituted Na+/K+ vesicles, commonly regarded as strong evidence. Just recall the experiments of Wiggins and MacClement [62] on ATP synthesis with cellulose acetate films.
What then is the function of Na+/K+-ATPase? The earlier discussion about the experiments with red cell ghosts (section 6: point 3) clearly indicates that Na+ exclusion and K+ accumulation depend on something located in cytoplasm, which depends on ATP. In the case of cell-matrix-filled red cell ghosts a good guess can be made. Ling showed that hemoglobin together with actin (both adsorb ATP) and a yet to be determined minor cell-matrix component are responsible for the amounts of Na+ and K+ in the red cell ghosts [12, 18, 19, 24-26]. The results obtained by the group of Kellermayer on entire red blood cells [121-123] and Lingís experiments with EMOC preparations [51] confirm that the cell-matrix is responsible for the amounts of both ions, and that their concentrations do not depend on the working of membrane-located Na+/K+-ATPase. However, in intact cells, Na+ and K+ ions have to pass through the plasma membrane and this suggests that Na+/K+-ATPase is responsible for the flux through the membrane, though not for the intracellular concentrations. It may even be a regulator of the flux, as indicated by the more recent insight that Na+/K+-ATPase has a receptor function [14, 133]. This function agrees with observations of its connectivity to the cytoskeleton [134, 135]. Its function is definitely not to maintain steady state energetics, as differences in Rb+ uptake and release rates in different types of red blood cells demonstrate [123]. In the latter study the conclusion was reached that Na+/K+-ATPase is involved in the uptake of Rb+ (K+), which can be inhibited by ouabain, but that the Rb+ (K+) distribution/content is not affected either by this enzyme or by ouabain. This indicates that the Rb+ (K+) distribution/content may be primarily defined by adsorption. Na+/K+-ATPase is therefore not an important player with respect to cell energetics, but cytoplasmic K+-adsorbing and water polarizing ATPases belonging to Lingís cell-matrix are.
Cell energetics is determined by the cell-matrix. Therefore, it may be important to clarify Lingís concept of the Ďcell-matrixí further. The results with cell-matrix-filled red cell ghosts and with EMOC preparations indeed suggest that something comparable to a pumping function (in the sense of Fröhlich) is connected to the cell-matrix. But there are four main differences from how MT sees pumping: (a) the activity is located in the cytoplasm with only a minor contribution from the plasma membrane; (b) the activity is only needed for a very short period, at the moment of the A-to-R transition, not all the time; (c) during the R-state a physical equilibrium is established with regard to ion and other solute distributions, instead of a ceaselessly energy-consuming steady state; (d) the energy stems from ATP adsorption and not from ATP hydrolysis [136].
Lingís [12, 18-26] definition of the cell-matrix as given earlier is a functional one. He is not primarily concerned with its morphology or composition. Certainly many proteins belonging to the cytoskeleton participate in the functions of the cell-matrix [18, 111] and many are ATPases or GTPases, but monomeric actin and tubulin, which may be only loosely interconnected, also polarize water and adsorb K+ [18], while they may act cooperatively via interspersed polarized water. Some membrane proteins and membrane surfaces also qualify for his definition [18]. So, there is no problem in seeing Na+/K+-ATPase as part of the cell-matrix, but this implies reckoning with the colloid context and the properties of associated water, and being open-minded with respect to membrane models [18].
In more recent work, Ling has coined the term Ďnano-protoplasmí [24, 26] (Matveev [132] used the term Ďphysiological atomí: the minimal structure that preserves the characteristic properties) in order to place more emphasis on the fact that the structural and functional units of life do not necessarily take up the entire cytoplasm or even large parts of it. They can be rather small. In a red blood cell, hemoglobin together with actin and the yet to be characterized minor protein may conform to the concept of cell-matrix and a minimal amount of it can yet be considered as nano-protoplasm. Fundamental to the definition of cell-matrix and nano-protoplasm is that its components Ė proteins, water and ions Ė possess Ďthe ability to exist as coherent assemblies in either one of two alternative states, the resting and active living (or dead) stateí [24].
This definition means that at a given moment certain parts of the cell may be active while others are inactive. Because during the period of activity new ATP is generated, and because in most cells many parts are active at a given moment, a cell may be continuously busy with ATP production. This situation may give a false impression of something like a steady state, fueling the metaphor of the burning candle. It may obscure the fact that some parts are literally inactive and hence not consuming energy at that moment. In that regard, studies of myofibrils or Artemia cysts are very instructive because a complete R-state can be obtained.
It should be realized that the R-state is difficult to study, because without specific measures important properties of the cell-matrix are lost by most in vitro preparatory methods and by the fixation methods used for light and electron microscopy. This makes correct interpretation of many experiments and also of many protein X-ray diffraction analyses very difficult. This has certainly helped to keep MT on the road. Perhaps MT is a good theory of a cell with a destroyed cell-matrix, capturing some aspects of the A-state but worth-less for the R-state.
To conclude, Lingís proposal [12, 18-26, 46] that it is not the hydrolysis of ATP that energizes cellular processes, but its adsorption to certain cell-matrix proteins, establishing a long-term (meta)-stable R-state without further energy consumption once established, is amply proven by his EMOC preparations. The red line on Fig. (1) depicts his view of cell energetics. The question to be addressed now is whether or not his energy model is complete? According to Ling it is. However, in his AIH almost nothing is said about globular proteins, although he agrees that they occur in vivo. Does their existence makes a difference for cell energetics? We think it does, although only in a secondary way. In our view thermodynamics of globular proteins can be described by the green line in Fig. (1); and this line has to be added to the view presented by Ling. Our view is based on Matveevís recent Ďnative aggregation hypothesisí (NAH).
8. Matveevís Native Aggregation Hypothesis (NAH)
Three aspects of Matveevís NAH [15] are of prime importance for this article. First, there is the work done by the school of Nasonov, to which he belongs, on some physical properties of the R-state and the A-state, demonstrating that R-to-A and A-to-R are indeed phase transitions. In this work the meaning of R- and A-states and their transitions is the same as in Lingís AIH (and incompatible with MT). Secondly, there is his idea of native aggregation as the universal mechanism for all kinds of physiological processes in living cells. Thirdly, there is his division of native proteins with respect to their in vivo conformation during the R-state into two well-defined groups from both a structural and an energetic point of view, the first group yielding the red line and the second group yielding the green line of Fig. (1). Addition of the second group allows the general outlines of an energy model, which fundamentally differs from the steady state model of MT, fully adopts Lingís entropic model, but adds some aspects linked to globular proteins.
Nasonov, like Ling, belonged to the small group of scientists who continued to believe in the bulk-phase nature of cells. Like Ling, he also studied the R-state of a living cell. This is a much-neglected field of inquiry, probably because nothing happens during the R-state and hence there is not very much to measure. The only way to learn about it is by comparison to the A-state. In this comparison some general physical parameters can be followed. Much of the work done appeared in the Russian language and as such it is largely unknown in the West. In his review of 2010 (in English), Matveev [15], a follower of Nasonov and also of Ling, summarized some main results of Nasonovís school, adding his own results and making the link with the work of Ling.
The school of Nasonov [10] studied the remarkable phenomenon that very different physical (pH, hydrostatic pressure, mechanical action) and chemical stimuli, when their intensity exceeds a certain threshold, are able to turn a resting cell (R-state) into an active one (A-state). It was found that all these different stimuli produce a similar set of general non-specific simultaneous changes in the physicochemical properties (viscosity, turbidity, hydrophobicity, structure) of very different types of living cells. Matveev [132] calls it Ďa universal reaction of the living cellí or Ďprotoreactioní.
Activation of the cell causes a biphasic transition. Macroscopic viscosity first decreases and then increases above the resting level; cytoplasm first becomes more transparent, then more turbid, exceeding the resting level; hydrophobicity of cytoplasm as studied by means of vital stains first decreases and then rises above the resting level; etc. The first step can be considered still part of the R-state, being a phenomenon below the activation threshold (as is the case for generator potentials in neurons). The second step is initiated when the cellís threshold is exceeded. It was called the Ďphase of excitationí and corresponds to the R-to-A transition discussed in this article. At the structural level, when a living cell is viewed in the light microscope, extensive optically empty regions look quite homogeneous while additional structures appear upon excitation, which are also seen after fixation. There is therefore some similarity between the excited state and the death (fixed) state. Both Ling [12] and Matveev [15] consider the death state to be an irreversible Ďover-activatedí state, whereas the physiological active state is always reversible. A pathological state, such as in cancerous cells, is in between: an over-activated yet reversible state (see also [104, 117]). In order to see the rather structure-less R-state in the electron microscope, special precautions are needed. A remarkably homogeneous and very fine gel-like structure can then be observed, described by Porter et al., [137] as the Ďmicrotrabecular latticeí. In contrast, procedures used in classical electron microscopy reveal some kind of over-activated death state [15, 71, 137] characterized by much coarser structures. All these properties of the activated situation in contrast to the resting situation are very reminiscent of what happens during in vitro aggregation of isolated (globular) proteins [138-140]. Hence, Nasonov formulated what he called Ďthe denaturational theory of cell excitation and damageí, which proposes that the cause of all the observed changes in physicochemical properties during cell activation has to be sought in stages of protein denaturation occurring in vivo.
Misunderstandings may arise because of the term Ďdenaturation of proteinsí. In many textbooks the word Ďdenaturationí is applied to globular proteins. In that case, denaturation proceeds by consecutive steps of unfolding until a completely unfolded random coil is obtained. This process is endothermic. Heat-denaturation is one of the methods for achieving it. According to Lingís AIH the cell-matrix during the R-state consists of a protein-water-ion complex with Ďfully-extendedí proteins. The structure of Porterís microtrabecular lattice [137] may be compatible with this notion. Matveev [15] gives a new quite literal definition of Ďdenaturationí, which allows the term also to be applied to the latter group of proteins. This new definition is intimately linked with the not yet widely-known concept of the R-state. The definition is derived from the idea that the Ďnativeí or Ďnaturalí state of a protein is how it occurs in the in vivo R-state. For a natively tightly-folded globular protein the act of denaturation then corresponds to the stages of unfolding. However, for a natively fully-extended protein, the act of denaturation corresponds to the process of folding. Matveev [15] expresses the latter idea as follows: ĎIn the native state the key cell proteins are inert, non-reaction-capable; they do not interact with each other or with other biopolymersí. That all proteins may be inactivated during the R-state is proved by the observations of Clegg on Artemia cysts [52]. In these cysts even glycolysis and respiration must have come to a halt: zero activity. And now the new definition: ĎLoss of the state of inertia is denaturationí [15]. When a fully-extended protein denatures (during R-to-A transition) temporary secondary structures appear and these structures are Ďreaction-capableí in a specific way. Specificity suddenly appears on stage. On the other hand, a tightly-folded globular protein is inert and non-reactive because its reactive structures, since they possess hydrophobic regions, are hidden in the interior of the globule. Upon activation they undergo partial melting producing an intermediate state, whereby the reactive structures become exposed, ready for specific interaction. So, when a tightly-folded globular protein partially denatures during R-to-A transition, this happens by slight melting, just enough to expose their reactive secondary structures and make them Ďreaction-capableí.
To begin with, the above description indicates that with respect to the process of denaturation and activation (the loss of the inert R-state), proteins fall into two well-defined groups: the natively fully-unfolded proteins described by Ling and hereafter called ĎNUN-proteinsí; and the natively tightly-folded proteins, corresponding to the more classical picture of a protein, at least a few decades ago, hereafter called ĎNF-proteinsí. This division is of prime importance for reaching an understanding of cell energetics because: (1) although the classical way of thinking about in vivo proteins has evolved quickly, it nevertheless remains strongly biased by MT and is incompatible with coherence and the in vivo state of water and K+, so wrong ideas about cell energetics are likely to persist for some time; (2) Lingís view takes away these problems with coherence and the in vivo state of water and K+, but in his cell-matrix concept he only describes NUN-proteins, devoting only a few sentences to globular proteins. For instance, in his 1992 book ([19], p. 72), he makes a clear distinction: ĎIn globular native proteins, hydration is limited to polar side chains. Ö In fibrous proteins, some of the backbone NH-CO groups are not locked in intra-macromolecular H-bonds, and are thus free to sorb water. Ö The polar side chains, as a rule, sorb relatively small amounts of waterí, whereas a few pages further (p. 100) he states about NUN-proteins:í ĎBoth water sorption in fully-extended proteins and that in living cells follow Bradleyís multilayer-adsorptioní. This reveals why he does not discuss NF-proteins very much. Indeed, in order to explain water-sorption by the entire cell, NF-proteins are rather irrelevant. He calculated that if all proteins were globular in the native state, only around 6.25% of cell water would be influenced. However, it will be argued below that NF-proteins do have a contribution in cellular energetic, although it is a secondary one.
Energetically the existence of two groups of proteins during the R-state, NUN- and NF-proteins, also follows from caloric measurements of protein unfolding. These studies reveal that the fully-folded state has a stability of between +20 to +80 kJ/mole [54] compared to the fully-unfolded state and so the unfolded state needs an external energy input in order to exist. In view of the AIH, the above energetic values make it clear that proteins that are closer to the lower value of +20 kJ/mole could exist in a largely unfolded state with an energy input derived from the adsorption of ATP, which is in the order of -45 kJ/mol [45, 124, 125]. These are NUN-proteins, characterized by a high-energy level. Their activation leads to folding, which is an exothermic process and allows power output. Owing to the adsorption and polarization of the surrounding water, the inactive ensemble of ATP-protein-water-ion has very low entropy. So, the power output is driven by entropy. Evidently, for proteins closer to the higher value of +80 kJ/mol, a fully-folded globular in vivo state is more likely. This state is stable by itself because it occupies a minimum energy well. Their active intermediate state, however, remains at a higher energy level and hence needs energy input (activation energy). These are the more classic globular or NF-proteins.
Modern protein biophysics supports the existence of rather stable and reproducible intermediate states separated by a threshold from other states, and situated between the two extremes of the tightly-folded globule and the fully unfolded protein [55]. Dunker et al. [141] proposed the concept of the Ďmolten globuleí and Uversky [142] of the Ďpremolten globuleí. Since the field is currently developing, preference is given here to the more general term Ďactive intermediateí state(s)í, particularly because the NAH deals with any kind of physiological process and not all cases need be similar. NAH holds that globular proteins are inactive in their most compact fully folded state hiding their reactive sites (the native state) and are activated by transition to a more loosened intermediate state, whereby the reactive sites are exposed to the surroundings and become reaction-capable. Activation of globular proteins by loosening their tightly folded state is evidently endergonic. It can be concluded that since the existence of globular proteins in vivo cannot be denied, neither does the endergonic nature of their activation, the green line in Fig. (1) has to be added.
What counts in favor of the concept of native aggregation is that (1) a given protein can exist in an inactive inert state and in one or more active functional states; (2) in the active state(s) interaction-capable secondary structures appear and can be exposed to other activated biomolecules (not necessarily only proteins, actually any kind of ligand) so that physiological activity can take place temporarily. The rationale of the NAH lies in the facts that (a) the specificity required for each individual kind of physiological process during the A-state does not exist during the R-state but appears at the beginning of the R-to-A transition through the mechanism of protein denaturation (new definition); (b) despite the many kinds of different stimuli and the huge variety of specific physiological responses, the common mechanism of protein denaturation (new definition) always goes along with the same non-specific or universal changes of all physicochemical parameters associated with a protein-water-ion phase transition; and (c) that the formation of functional aggregates is not the result of a random Brownian process (as described in the literature on IDPs [56]), but is an organized event in agreement with the literature on coherence (see before) and with Cosicís resonance recognition model [83, 84]. For a further more detailed treatment of these concepts including a number of clarifying examples reference [15] can be consulted.
Summarizing in Matveevís words [15]: ĎTwo extreme protein states can be identified: the completely folded (the globular protein) and the completely unfolded states. Between these inactive (native) states, numerous intermediate, active forms can exist; it is these forms that produce native aggregation.í
9. A New Proposal (Model) for Cell Energetics
This new proposal, based on Lingís AIH and extended by Matveevís NAH, is depicted in Fig. (1). The red line is for NUN-proteins (see before: section 4 point 1) and the green line for NF-proteins. Below a complete overview for each stage from R over to A and back to R is given.
The R-state
Considering the entire living cell, the R-state is a metastable
high-energy low-entropy state, stable over long periods of time, as EMOC
preparations [51] and Cleggís work on Artemia cysts [52] made clear.
The term Ďmetastableí is used to indicate the stability of the
high-energy character of the R-state, but also its potential to fall into
lower-energy states, because it is very far from thermodynamic equilibrium (see
[143] for details). However, as Ling [51] pointed out with his EMOC
preparations, it is nevertheless a physical equilibrium, in need of neither
pumping activity nor a continuous energy supply, as MT erroneously believed. The
R-state can exist in a high energy basin, so a small amount of external energy
is needed to leave this basin. This small amount can be regarded as a kind of
activation energy, delivered for instance by the adsorption energy of
activating cardinal adsorbents such as Ca2+ (or another activator).
The amount of energy introduced by the external stimulus must be sufficient to
reach the threshold; if not, the R-state persists.
In the late 1960s, Prigogine [144] developed the thermodynamics of non-linear systems far from equilibrium and characterized by dynamic behavior. He discussed living systems from his new point of view. During activity (R-to-A and A-to-R transitions), living systems are indeed dynamic, so his thermodynamics could be applied. If MT were correct, these thermodynamics would also apply to the R-state, since MT regards the R-state as a steady state in need of continuous pumping activity, i.e. as a dynamic system. However, as explained above, Ling demonstrated beyond doubt that MT is wrong and that the R-state is a metastable static state, in physical equilibrium but far from thermodynamic equilibrium. This means that the thermodynamics of Prigogine cannot be used to describe the R-state. Only very recently, Prokhorenko and Matveev [143] derived the thermodynamics of static (metastable) non-linear systems far from equilibrium. They were developed from first principles and immediately applied to Lingís description of a cellís R-state. Lingís R-state has therefore been placed on a firm thermodynamic foundation.
In the late 1960s, Prigogine [144] developed the thermodynamics of non-linear systems far from equilibrium and characterized by dynamic behavior. He discussed living systems from his new point of view. During activity (R-to-A and A-to-R transitions), living systems are indeed dynamic, so his thermodynamics could be applied. If MT were correct, these thermodynamics would also apply to the R-state, since MT regards the R-state as a steady state in need of continuous pumping activity, i.e. as a dynamic system. However, as explained above, Ling demonstrated beyond doubt that MT is wrong and that the R-state is a metastable static state, in physical equilibrium but far from thermodynamic equilibrium. This means that the thermodynamics of Prigogine cannot be used to describe the R-state. Only very recently, Prokhorenko and Matveev [143] derived the thermodynamics of static (metastable) non-linear systems far from equilibrium. They were developed from first principles and immediately applied to Lingís description of a cellís R-state. Lingís R-state has therefore been placed on a firm thermodynamic foundation.
Proteins making up the R-state must now be dissected into the two groups described above. NUN-proteins making up Lingís cell-matrix are responsible for the fact that the R-state is a metastable high-energy low-entropy state. The stability of their association with bound ATP is responsible for the static character of this state, whereas the process of ATP binding during an A-to-R transition is responsible for lifting the system into the high-energy low-entropy basin. NF-proteins are stable on their own during the R-state, since they exist in the fully folded conformation, which for proteins represents the minimum energy basin. Summation of the energy levels of the two groups gives the high-energy level of the entire system in the R-state. It equals the energy level of NUN-proteins minus the energy level of NF-proteins. The result of this summation in all cases remains in favor of a net high-energy level.
R-to-A transition
R-to-A transition is initiated by an external stimulus or internal
signal of sufficient strength to overcome the threshold. It is relayed to the
appropriate intracellular site mostly indirectly, for instance mediated by Ca2+.
The latter in turn acts on NUN-proteins that bear cardinal adsorption sites for
activation (for instance Ca2+-binding sites). The strong inductive
effect exerted by this binding is auto-cooperatively transmitted through the
cooperatively-linked cell-matrix (NUN-protein system) and unleashes non-specific
effects associated with the R-to-A phase transition, together with a whole range
of specific functional effects, which are dependent on specific interactions
among specific proteins (see NAH).
Again, the two groups of proteins have to be distinguished. Folding of NUN-proteins is exergonic, whereby dissociation and depolarization of associated water and desorption of bound K+ are responsible for a large increase in entropy. Power output is generated from the stored low entropy. The slight unfolding of NF-proteins into an active intermediate conformation, however, is endergonic. It is proposed in this new model that the necessary energy is transferred from the exergonic reaction of NUN-proteins to NF-proteins. Mechanisms for such energy transfer will be given at the end of this article. The net exergonic nature of the R-to-A transition for the entire system is equal to the energy liberated by NUN-proteins minus the energy uptake by NF-proteins and always has a net exergonic character, so that power output is guaranteed.
Native aggregation is a broad concept dealing with the temporary formation of active functional complexes of proteins with any kind of ligand (other proteins, polynucleotides, substrates, ions, etc.) at the onset of R-to-A transition [15]. Formation of an aggregate of two or more NUN-proteins (for instance, actomyosin formation) is exothermic, of a NUN-protein with a NF-protein is net exothermic. Interaction between two NF-proteins is not excluded, but energetically it is only possible after the activation energy for both proteins is delivered in some way, whereby ultimately this energy must come from the R-to-A transition of a NUN-protein system or directly from an external stimulus.
The A-state
In the A-state NUN-proteins and NF-proteins are in a quite
different situation. Actin and myosin can be taken as examples of cell-matrix
(NUN-) proteins [12, 14, 18, 70, 73, 134]. They possess unfolded regions [14,
75], polarize water [14, 18, 73], adsorb K+ [68-73], possess cardinal
adsorption sites for ATP and exhibit ATPase activity [12, 14]. It was shown that
upon activation of myofibrils weak binding between the S1-head of
myosin and actin is followed by the release of Pi , allowing strong
binding, which in turn leads to the power stroke and only then to ADP-release
[145]. Together, these consecutive steps represent the R-to-A transformation,
which is an exergonic dynamic process. After dissociation of ADP the system
settles into its stable (static) low-energy basin, the A-state (rigor) with
myosin heads free of nucleotides. Myofibrils will remain in this rigor state
unless ATP is added [76, 145]. This fact illustrates the static and stable
nature of the A-state as far as it concerns NUN-proteins. In contrast, during
the A-state NF-proteins may remain active as they occur in a high-energy
functional state, described above as an active intermediate state. The
energy to lift NF-proteins into their active intermediate state can be
considered as a kind of activation energy and should be delivered either
directly from the stimulus or from the R-to-A transition of NUN-proteins.
Mechanisms of energy transfer are described below.
Summing up, the A-state has both a static low-energy component of NUN-proteins and a dynamic (relatively) high-energy component of NF-proteins. The high-energy level of NF-proteins during the A-state is, however, lower than the high-energy level of NUN-proteins during the R-state, so that the R-to-A transition is invariably exergonic.
A-to-R transition
Glycolysis and respiration generate new ATP. Some ATP is needed to
activate these pathways (for instance hexokinase and phosphofructokinase
reactions) before a larger amount of ATP can be generated. Therefore a cell
always needs a minimal amount of ATP (see also EMOC experiments). In a healthy
cell the minimal requirement for ATP remains sufficient during the A-state so
that metabolic activity generates more ATP, lowering the ADP/ATP ratio. This new
ATP quickly adsorbs to NUN-proteins of the cell-matrix because of the very high
adsorption coefficients for these proteins (for actomyosin: 9.8x106
[46]). The adsorption energy of ATP (near 45kJ/mol) lifts NUN-proteins of the
cell-matrix back into their inactive (meta)stable high-energy low-entropy basin
of the R-state. As stated earlier, Ling made it unequivocally clear that the
adsorption energy and not the hydrolysis energy of ATP is responsible for this
A-to-R transition [12, 18-26, 46]. NF-proteins may return to their low-energy
inactive fully folded state by means of several mechanisms discussed below.
Their inactivation per se is exergonic, but eventually a small amount of energy
is needed to reach the border of the high-energy basin they occupy. Whether or
not this small amount is needed may depend on the particular case; therefore,
two dotted green lines are drawn for this stage on Fig. (1). It depends whether
the activated state is a real energy basin or a transient that needs only
activation energy to start it, in which case it then flows exothermically
downwards.
Energy Transfer between NUN- and NF-proteins
While the need to activate NF-proteins during R-to-A transition is
self-evident, as explained above, the source of the energy is rather speculative
in the sense that there are many possibilities and there might be different
mechanisms for different cases. Activation energy for NF-proteins may be
delivered either (a) rather directly from the stimulus itself or (b) indirectly
from the stimulus through the intermediary of a NUN-system. In the latter case,
the question is: how is energy transferred from a NUN-system to a NF-system?
First, this energy transfer may occur when direct conformational contact is possible between proteins of the two groups. Many globular (NF) proteins are thought to be associated with elements of the cell-matrix (NUN-proteins) [111], enabling such direct transfer. Molecules of some proteins have both NF-segment(s) and NUN-segment(s) at the time [58]. Alternatively, energy could be tapped from the immediate surroundings. Indeed the most penetrating aspects of the R-to-A phase transition are due to the NUN-system. The local physicochemical environment is changed so profoundly and in an exothermic entropy-generating way that a nearby inactive NF-protein has plenty of energy in its immediate vicinity to be activated. The cooperative transformation of Ling's resting protein-water-K+ complex indeed results in a change of the physical conditions in protein microenvironments. The region that was previously in its R-state becomes more permeable. Diffusive fluxes of substances appear and with them come gradients of thermodynamic potentials: the higher the degree of cooperativity, the greater those potential gradients. In the case of ions, electric diffusion potentials are generated. These potentials can be energy sources for any kind of biological work including melting of some globular proteins. Proteins have side groups that vary greatly in polarity. This means that proteins are surface-active compounds. Living cells, as colloidal systems, exhibit many local phases and interphase boundaries. Interphase boundaries are surfaces for the adsorption of various substances, including proteins. Phase transitions fundamentally change the distribution of substances in the A-state as compared to the R-state. This may lead to changes in adsorption/desorption. The energy associated with these adsorption/desorption processes may easily destabilize a proteinís R-state and lead to melting of NF-proteins or to folding of (a new portion of) a NUN-protein.
Energy transfer over longer distances is also possible, for instance by shuttling of allosteric modulators, second messengers, or ions. Some other mechanisms of energy transfer over longer distances are often of a coherent type: short or long distance transmission of energetic pulses along auto-cooperatively linked protein systems such as microfilaments or microtubules. Davydov-solitons and electro-solitons have been suggested for energy transfer along these transmission lines [92-94]. Biophotons may constitute another mechanism for long-distance transmission and coordination [103-105]. At a more local level Cosicís resonance recognition model [83, 84] may be of particular importance.
Glycolysis, Respiration and the K+-shuttle
The energy model depicted on Fig. (1) is finalized with a proposal
of (a) the likely mechanism of activation of the ATP regenerating system as the
R-to-A transition proceeds; and (b) the mechanism of its de-activation as the
R-state is reinstalled. A causative time sequence of events is proposed as the
most obvious mechanism. In this proposal the R-to-A transition of for instance
actin and myosin starts earlier than the R-to-A transition for ATP synthesis,
because the latter has to wait upon liberation of ADP from actin [146] and
myosin [145, 146]. Similarly, subsequent adsorption of new-ly formed ATP to
actin and myosin [124, 125, 145, 146] restoring the R-state of the latter
proteins precedes the inac-tivation of the ATP synthesizing machinery, because
the latter has to wait the lowering of the ATP/ADP ratio caused by the ATP
adsorption process (see Fig. 1).
This proposal might look strange when one has the impression that ATP and ADP are distributed rather homogeneously in Ďcytosolí and that ATP synthesis and consumption take place continuously, be it at a physiologically adaptable speed. However, the co-existence of R- and A-states simultaneously in different parts of the cell together with the amphipatic properties of nucleotides necessitate to leave the idea that free ATP is present all over the Ďcytosolí and is synthesized permanently. The high value of the adsorption coefficient of ATP to certain proteins makes its free concentration in cellular regions, which are in the R-state almost nihil; and glycolysis is likely to be halted in that region. At the end of R-to-A transition the sudden local liberation of ADP must lead to a local quantitative conversion into new ATP, which then adsorbs fast and locally. In this story K+ may play a primary role.
The key regulatory function of K+ during the R-to-A-to-R cycle is not generally realized. In a recent extensive review of the role of monovalent ions in enzyme function, Page and Di Cera [147] wrote: ĎBecause the concentration of Na+ and K+ is tightly controlled in vivo, M+ Ďs do not function as regulators of enzyme activityí. Contrarily, according to Lingís AIH, K+ activity is quite different between the R- and A-states, so K+ may effectively exert a regulatory function of prime importance. Ling [148] proposed such regulation in an un-cited short paper. K+ activity is very low during the R-state (about 2.5 mM) owing to adsorption to NUN-proteins of the cell-matrix. This bound K+ is then suddenly liberated at the onset of the R-to-A transition yielding a high K+ activity (about 150mM in neurons) during the A-state. Some of the liberated K+ ions may subsequently bind to some other proteins. Ling [148] mentions that two metabolic pathways in particular are activated by high K+ activity: glycolysis and respiration. Pyruvate kinase [149, 150] absolutely requires high K+ activity and so does phosphofructokinase [151]. Mitochondrial activation is dependent on a K+ influx [152-155], which according to the AIH is initiated at the onset of the R-to-A transition. At that moment, K+ may literally turn on these pathways as a main switch; and next, an increasing ADP/ATP ratio, associated with the power output of the R-to-A transition, further modulates the pathway flux in an allosteric way. In addition, increased ADP and Pi activity have a substrate effect on these pathways. As a result new ATP is quickly generated and binds to nearby NUN-proteins. This reinstalls the R-state of this group, whereby K+ is re-adsorbed. K+ activity drops again to a low value, causing its dissociation from regulatory glycolytic enzymes and leaving mitochondria. Glycolysis and respiration are again inactivated. If a cell is at complete rest, low K+ activity in the entire cell may lead to complete shutdown of glycolysis, respiration and other metabolic pathways. The total ATP concentration in the cell is high, but it is adsorbed to NUN-proteins in a stable manner. This at least follows from Cleggís observations on Artemia cysts [52]. It is therefore time to realize that great changes in K+ activity during R-to-A and A-to-R transitions may operate as a real ON/OFF switch for ATP-generating pathways.
Considering the entire R-to-A-to-R cycle, the effects of K+ may give rise to an automatic causative time sequence mechanism enabling the cycle to proceed and limiting the duration of the A-state, possibly also in the case of Ďlimit cyclesí, where cytoplasmic K+ oscillations may be expected. Mitochondrial K+ cycling has been described [155], but unfortunately it was not interpreted from Lingís point of view, as has been done here.
CONCLUSIONS
Schrödingerís idea that Ďlife feeds on negative entropyí [17] could not find its place in MT because, according to MT, the media on both sides of the plasma membrane do not differ in entropy (ions and water are thought to be free on both sides). MT has therefore been the greatest obstacle to the spread of physical ideas and methods in cell physiology. As a result, there is a huge gap between cell physiology and both physics and chemistry (especially colloid chemistry). It is clear that the living cell is a multiphase system with many interfaces including the surfaces of proteins, protein complexes, and different supra-molecular structures. For most biologists the term Ďcolloidí is associated with the early 20th century. However, during the past two decades, colloid chemistry has developed a great deal. The knowledge obtained must now be used to solve problems of cell physiology. Biologists, who are working with colloidal systems (cells and cell models) but possibly not realizing it, may draw erroneous conclusions if they lack knowledge of physical and colloid chemistry. What seems to have been proven may be a serious mistake. It is necessary to combine the efforts of scientists from various specialties. Lingís AIH is a good springboard for physicists who are interested in biology. But even more, everybody working in biosciences should have knowledge of Lingís AIH, Pollackís GSH and the coherent behavior of cells. An alternative view of such broad extent and importance including a different view of cellular energetic, expanded slightly by the present study, should not be missing from general textbooks and basic university courses.
ABBREVIATIONS
A =
Action
AIH =
Association-induction hypothesis
EMOC = Effectively membrane-(pump)-less
open-ended muscle cells
GSH = Gel-sol
hypothesis
HDW = High-density water
LDW = Low-density water
MT =
Membrane theory
NAH = Native aggregation
hypothesis
PML-water = Polarized
multilayer water
R
= Rest(ing);
NF-proteins = Natively folded globular
proteins
NUN-proteins = Natively unfolded proteins
CONFLICTS OF INTEREST
The authors confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENTS
We are indebted to Paul Agutter and Ludwig Edelmann for valuable comments and to Paul Agutter for stylistic improvements.
REFERENCES
[1] Pfeffer, W.F. Osmotische Unterzuchungen: Studien zur Zell-Mechanik, 2nd ed.;
Englemann: Leipzig, 1921.
[2] Hill, A.V.
The state of water in muscle and blood and the osmotic behaviour
of muscle. Proc. R. Soc. London Ser. B, 1930, 106, (746), 477-505.
[3] Hill, A.V.; Kupalov, P.S.
The vapour pressure of muscle. Proc. R. Soc.
London Ser. B, 1930, 106 (746), 445-477.
[4] Dean, R. Theories of electrolyte equilibrium in muscle. Biol. Symp., 1941,
3, 331-348.
[5] Rosenberg, T. The concept and definition of active transport. Symp. Soc.
Exp. Biol., 1954, 8, 27-41.
[6] Ussing, H.H. Transport of ions across cellular membranes. Physiol. Rev.,
1949, 29 (2), 127-155.
[7] Hodgkin, A.L.; Huxley, A.F.
Currents carried by sodium and potassium ions
through the membrane of the giant axon of Loligo. J. Physiol., 1952, 116 (4),
449-472.
[8] Lipmann, F.
Metabolic generation and utilization of phosphate bond energy.
Adv. Enzymol., 1941, 1, 99-162.
[9] Gortner, R.A.; Gortner, W.A.
The cryoscopic method for the determination of
Ďbound waterí. J. Gen. Physiol., 1934, 17 (3), 327-339.
[10] Nasonov, D.N.
Local Reaction of Protoplasm and Gradual Excitation. (English Transl. by
Halpern, Y.S.), National Science Foundation, available at Office of Technical
Services, Department of Commerce, US: Washington, D.C., 1962.
[11] Ling, G.N.
A Physical Theory of the Living State: the Association-Induction
Hypothesis. Blaisdell: Waltham, Massachusetts, 1962.
[12] Ling, G.N.
Life at the Cell and Below-Cell Level. The Hidden History of a Fundamental
Revolution in Biology. Pacific Press: New York, 2001.
[13] Troshin, A.S.
Problems of Cell Permeability. Widdas W.F., Ed. (English Transl. by Hell,
M.G.). Pergamon Press: London, 1966.
[14] Pollack, G.H.
Cells, Gels and the Engines of Life. A New, Unifying Approach to Cell Function.
Ebner & Sons: Seattle, 2001.
[15] Matveev, V.V.
Native aggregation as a cause of origin of temporary cellular structures needed
for all forms of cellular activity, signalling and transformations. Theor.
Biol. Med. Model., 2010, 7, 19.
[16] Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P.
Molecular Biology of the Cell, 4th ed.; Garland Science: New York, 2002.
[17] Schrödinger, E. What is Life? The Physical Aspect of the Living Cell.
Cambridge University Press: Cambridge, 1944. Canto edition, Cambridge University
Press: Cambridge, 1992.
[18] Ling, G.N.
In Search of the Physical Basis of Life. Plenum Press: New York, 1984.
[19] Ling, G.N.
A revolution in the physiology of the living cell. Krieger Publ. Co.:
Malabar, Florida, 1992.
[20] Ling, G.N.
A new theoretical foundation for the polarized-oriented multilayer theory of
cell water and for inanimate systems demonstrating long-range dynamic
structuring of water molecules. Physiol. Chem. Phys. Med. NMR, 2003, 35 (2),
91-130.
[21] Ling, G.N.
What determines the water content of a living cell? Physiol.
Chem. Phys. Med. NMR, 2004, 36 (1), 1-19.
[22] Ling, G.N.
An updated and further developed theory and evidence for the
close-contact, one-on-one association of nearly all cell K+ with
beta- and gamma-carboxyl groups of intracellular protein. Physiol. Chem. Phys.
Med. NMR, 2005, 37 (1), 1-63.
[23] Ling, G.N.
An ultra simple model of protoplasm to test the theory of its
long-range coherence and control so far tested (and affirmed) mostly on intact
cell(s). Physiol. Chem. Phys. Med. NMR, 2006, 38 (2), 105-145.
[24] Ling, G.N.
Nano-protoplasm: the ultimate unit of life. Physiol. Chem. Phys. Med. NMR,
2007, 39 (2), 111-234.
[25] Ling, G.N.
History of the membrane (pump) theory of the living cell from its beginning in
the mid-19th century to its disproof 45 years ago Ė though still thought
worldwide today as established truth. Physiol. Chem. Med. Med. NMR, 2007, 39
(1), 1-67.
[26] Ling, G.N.
A historically significant study that at once disproves the membrane (pump)
theory and confirms that nano-protoplasm is the ultimate physical basis of life
Ė yet so simple and low-cost that it could easily be repeated in many high
school biology classrooms worldwide. Physiol. Chem. Phys. Med. NMR, 2008, 40
(2), 89-113.
[27] Skou, J.C.
Nobel Lecture. The identification of the sodium pump. Biosci.
Rep., 1998, 18 (4), 155-169.
[28] Hoffman, J.F.
The link between metabolism and active transport of
sodium in
human red cell ghosts. J. Membr. Biol., 1980, 57 (2), 143-161.
[29] Hilden, S.; Rhee; H.M.; Hokin, L.E.
Sodium transport by phospholipid
vesicles containing purified sodium and potassium ion-activated adenosine triphosphatase. J. Biol. Chem., 1974, 249 (23), 7432-7440.
[30] Glynn, I.M.; Karlish, S.J.
The sodium pump. Annu. Rev. Physiol., 1975, 37
13-55.
[31] Hazlewood, C.F. Physicochemical state of ions and water in living tissues
and model systems. Ann. N. Y. Acad. Sci., 1973, 204, (1), 1-631.
[32] Ling, G.N.; Miller, C.; Ochsenfeld, M.M.
The physical state of solutes and
water in living cells according to the association-induction hypothesis. Ann. N.
Y. Acad. Sci., 1973, 204 (1), 6-50.
[33] Scott, D.M.
Sodium cotransport systems: cellular, molecular and regulatory
aspects. Bioessays, 1987, 7 (2), 71-78.
[34] Ling, G.N.
Active transport across frog skin and epithelial cell systems
according to the association-induction hypothesis. Physiol. Chem. Phys., 1981,
13 (4), 356-382.
[35] Post, R.L.; Jolly, P. The linkage of sodium, potassium and ammonium active
transport across the human erythrocyte membrane. Biochim. Biophys. Acta, 1957,
25 (1), 118-128.
[36] Ling, G.N.
The cellular resting and action potentials: interpretation based
on the association-induction hypothesis. Physiol. Chem. Phys., 1982, 14 (1),
47-96.
[37] Cope, F.W. Solid state physical replacement of Hodgkin-Huxley theory. Phase
transformation kinetics of axonal potassium conductance. Physiol. Chem. Phys.,
1977, 9 (2), 155-160.
[38] Edelmann, L.
The influence of rubidium and cesium ions on the resting
potential of guinea-pig heart muscle cells as predicted by the
association-induction hypothesis. Ann. N. Y. Acad. Sci., 1973, 204 (1), 534-537.
[39] Tasaki, I. Evidence for phase transition in nerve fibers, cells and
synapses. Ferroelectrics, 1999, 220 (1), 305-316.
[40] Mitchell, P.
Chemiosmotic coupling in oxidative and photosynthetic
phosphorylation. 1966. Biochim. Biophys. Acta, 2011, 1807 (12), 1507-1538.
[41] Williams, R.P.J.
The problem of proton transfer in membranes. J. Theor.
Biol., 2002, 219 (3), 389-396.
[42] Ling, G.N.
Oxidative phosphorylation and mitochondrial physiology: a critical review of
chemiosmotic theory, and reinterpretation by the association-induction
hypothesis. Physiol. Chem. Phys., 1981, 13 (1), 29-96.
[43] Kell, D.B. On the functional proton current pathway of electron transport
phosphorylation. An electrodic view. Biochim. Biophys. Acta, 1979, 549 (1),
55-99.
[44] Kell, D.B.; Hitchens, G.D. Coherent properties of the membranous systems of
electron transport phosphorylation. In Coherent excitations in biological
systems. Fröhlich, H.; Kremer, F., Eds.; Springer-Verlag: Heidelberg, 1983; pp.
178-198.
[45] Glynn, I.M.
A hundred years of sodium pumping. Ann. Rev. Physiol., 2002,
64, 1-18.
[46] Ling, G.N.
The physical state of water in living cells and model systems. Ann. N. Y.
Acad. Sci., 1965, 125 (2), 401-417.
[47] Giguère, P.A.; Harvey, K.B.
On the infrared absorption of water and heavy
water in condensed states. Canad. J. Chemistry, 1956, 34 (6), 798-808.
[48] Ise, N.; Konishi, T.; Tata, B.V.R.
How homogeneous are ďhomogeneous
dispersionsĒ? Counterion-mediated attraction between like-charged species.
Langmuir, 1999, 15 (12), 4176-4184.
[49] Ho, M.-W. The Rainbow and the Worm. The Physics of Organisms, 3rd ed.;
World Scientific: Singapore, London, 2007.
[50] Zheng, J.M.; Pollack, G.H.
Long-range forces extending from polymer-gel
surfaces. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys., 2003, 68 (3 Pt.1),
031408-031414.
[51] Ling, G.N. Maintenance of low sodium and high potassium levels in resting
muscle cells. J. Physiol., 1978, 280 (1), 105-123.
[52] Clegg, J.S. Embryos of Artemia franciscana survive four years of
continuous anoxia: the case for complete metabolic rate depression. J. Exp.
Biol., 1997, 200 (Pt.3), 467-475. Recent paper: Clegg 2011 The unusual response
of encysted embryos of the animal extremophile, Artemia franciscana, to
prolonged anoxia.
[53] Ling, G.N. The role of inductive effect in cooperative phenomena of
proteins. Biopolym. Symp., 1964, 13, 91-116.
[54] Wright, P.E.; Dyson, H.J.
Intrinsically unstructured proteins: re-assessing
the protein structure-function paradigm. J. Mol. Biol., 1999, 293 (2), 321-331.
[55] Finkelstein, A.V.; Ptitsin, O.B. Physics of proteins. Academic Press:
Amsterdam, 2002.
[56] Wright, P.E.; Dyson, H.J.
Linking folding and binding. Curr. Opin. Struct.
Biol., 2009, 19 (1), 31-38.
[57] Uversky, V.N.; Dunker, A.K.
Understanding protein non-folding. Biochim.
Biophys. Acta, 2010, 1804 (6), 1231-1264.
[58] Chouard, T.
Structural biology: breaking the protein rules. Nature, 2011,
471, (7337), 151-153.
[59] Chaplin, M.F.
A proposal for the structuring of water. Biophys. Chem.,
2000, 83 (3), 211-221.
[60] Chaplin, M.
Do we underestimate the importance of water in cell biology?
Nat. Rev. Mol. Cell Biol., 2006, 7 (11), 861-866.
[61] Wiggins, P.
Life depends upon two kinds of water. PLoS One, 2008, 3 (1),
e1406.
[62] Wiggins, P.M.; MacClement, B.A.
Two states of water found in hydrophobic
clefts: their possible contribution to the mechanisms of cation pumps and other
enzymes. Int. Rev. Cytol., 1987, 108 249-303.
[63] Kaivarainen, A.
Hierarchic theory of matter, general for liquids and
solids: ice, water and phase transitions. AIP Conf. Proc., 2001, 573 (1),
181-200.
[64] Edelmann, L.
The physical state of potassium in frog skeletal muscle studied by ion-sensitive
microelectrodes and by electron microscopy: interpretation of seemingly
incompatible results. Scanning Microsc., 1989, 3 (4), 1219-1230.
[65] Huang, H.W.; Hunter, S.H.; Warburton, W.K.; Moss, S.C.
X-ray absorption
edge fine structure of potassium ions in various environments: application to
frog blood cells. Science, 1979, 204 (4389), 191-193.
[66] Damadian, R.; Cope, F.W. Potassium nuclear magnetic resonance relaxations
in muscle and brain, and in normal E. coli and a potassium transport mutant.
Physiol. Chem. Phys., 1973, 5, (6), 511-514.
[67] Cope, F.W.; Damadian, R. Biological ion exchanger resins. IV. Evidence for
potassium association with fixed charges in muscle and brain by pulsed nuclear
magnetic resonance of 39K. Physiol. Chem. Phys., 1974, 6 (1), 17-30.
[68] Ling, G.N.; Ochsenfeld, M.M.
Studies on ion accumulation in muscle cells.
J. Gen. Physiol., 1966, 49 (4), 819-843.
[69] Kellermayer, M.; Ludany, A.; Jobst, K.; Szucs, G.; Trombitas, K.; Hazlewood,
C.F.
Cocompartimentalisation of proteins and K+ within the living
cell. Proc. Natl. Acad. Sci. USA, 1986, 83 (4), 1011-1015.
[70] Edelmann, L.
Basic biological research with the striated muscle by using cryotechniques and
electron microscopy. Physiol. Chem. Phys. Med. NMR, 2001, 33 (1), 1-21.
[71] Edelmann, L.
Freeze-dried and resin-embedded biological material is well suited for
ultrastructure research. J. Microsc., 2002, 207 (Pt.1), 5-26.
[72] Edelmann, L.
Potassium binding sites in muscle: electron microscopic
visualization of K, Rb, and Cs in freeze-dried preparations and autoradiography
at liquid nitrogen temperature using 86Rb and 134Cs.
Histochemistry, 1980, 67 (3), 233-242.
[73] Tigyi, J.; Kallay, N.; Tigyi-Sebes, A.; Trombitas, K. Distribution and
function of water and ions in resting and contracted muscle. In 2nd Int. Symp.
Cell Biology. Schweiger H.G., Ed.; Springer: Berlin, 1980; pp. 924-940.
[74] Jaeken, L. The coherence of life: building a new paradigm for cell
physiology. Relevance for oxidative phosphorylation. Biol. Bull., 2006, 16 11.
[75] Volkmann, N.; Hanein, D.
Actomyosin: law and order in motility. Curr. Opin.
Cell Biol., 2000, 12 (1), 26-34.
[76] Goldman, Y.E.; Hibberd, M.G.; McCray, J.A.; Trentham, D.R.
Relaxation of
muscle fibres by photolysis of caged ATP. Nature, 1982, 300 (5894), 701-705.
[77] Fröhlich, H.
Long-range coherence and energy storage in biological systems.
Int. J. Quantum Chem., 1968, 2 (5), 641-649.
[78] Fröhlich, H.
Long-range coherence and the action of enzymes. Nature, 1970,
228 (5276), 1093.
[79] Fröhlich, H.
The extraordinary dielectric properties of biological
materials and the action of enzymes. Proc. Natl. Acad. Sci. USA, 1975, 72 (11),
4211-4215.
[80] Fröhlich, H. Coherence in biology. In Coherent Excitations in Biological
Systems. Fröhlich H.; Kremer F., Eds.; Springer-Verlag, Berlin: Heidelberg,
1983; pp. 1-5.
[81] Fröhlich, H. General theory of coherent excitations in biological systems.
In Nonlinear Electrodynamics in Biological Systems. Adey W.R.; Lawrence A.F.,
Eds.; Plenum: New York, 1984; pp. 491-496.
[82] Fröhlich, H. Coherent excitations in active biological systems. In Modern
Bioelectrochemistry. Gutmann F.; Keyzer H., Eds.; Plenum: New York, 1986; pp.
246-261.
[83] Cosic, I.
Macromolecular bioactivity: is it resonant interaction between
macromolecules? Theory and applications. IEEE Trans. Biomed. Eng., 1994, 41
(12), 1101-1114.
[84] Ciblis, P.; Cosic, I.
The possibility of soliton/exciton transfer in
proteins. J. Theor. Biol., 1997, 184 (3), 331-338.
[85] Jaeken, L.
Linking physiological mechanisms of coherent cellular behavior
with more general physical approaches towards the coherence of life. IUBMB Life,
2006, 58 (11), 642-646.
[86] Vitiello, G.; Del Giudice, E.; Doglia, S.; Milani, M. Boson condensation in
biological systems. In Nonlinear Electrodynamics in Biological Systems. Adey
W.R.; Lawrence A.F., Eds.; Plenum: New York, 1984; pp. 469-476.
[87] Davydov, A.S.; Kislukha, N.I.
Solitary excitations in one-dimensional
molecular chains. Phys. Stat. Sol. (b), 1973, 59 (2), 465-470.
[88] Davydov, A.S.
Solitons and energy transfer along protein molecules. J. Theor. Biol., 1977, 66 (2), 379-387.
[89] Davydov, A.S.; Antonchenko, V.Ya.; Zolotariuk, A.V. Solitons and proton
motion in ice. Preprint ITP-81-60R, 1981. Institute for Theoretical Physics,
Kiev (in Russian).
[90] Davydov, A.S.; Zolotariuk, A.V.
Electrons and excitons in nonlinear
molecular chains. Phys. Scr., 1983, 28, 249-256.
[91] Scott, A.C. Solitary waves in biology. In Nonlinear Excitations in
Biomolecules. Peyrard M., Ed.; Springer-Verlag: Berlin, 1995; pp. 249-268.
[92] Hameroff, S.R. Ultimate Computing: Biomolecular Consciousness and
Nanotechnology. North-Holland: Amsterdam, 1987.
[93] Hameroff, S.R.; Watt, R.C.
Information processing in microtubules. J. Theor. Biol., 1982, 98 (4), 549-561.
[94] Bandyopadhyay, A. Experimental studies on a single microtubule:
investigation of electronic transport properties.
Google Workshop on Quantum Biology, Oktober 22, 2010.
[95] Heimburg, T.; Jackson, A.D.
On soliton propagation in biomembranes and
nerves. Proc. Natl. Acad. Sci. USA, 2005, 102 (28), 9790-9795.
[96] Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. Collective properties
of biological systems: solitons and coherent electric waves in a quantum field
theoretical approach. In Modern Bioelectrochemistry. Gutmann F.; Keyzer H.,
Eds.; Plenum: New York, 1986; pp. 263-287.
[97] Del Giudice, E.; Preparata, G.; Vitiello, G.
Water as a free electric
dipole laser. Phys. Rev. Lett., 1988, 61 (9), 1085-1088.
[98] Del Giudice, E.; De Ninno, A.; Fleischmann, M.; Mengoli, G.; Milani, M.;
Talpo, G.; Vitiello, G.
Coherent quantum electrodynamics in living matter. Electromagn. Biol. Med., 2005, 24 (3), 199-210.
[99] Del Giudice, E.; Elia, V.; Tedeschi, A.
Role of water in the living
organisms. Neural Netw. World, 2009, 19 (4), 355-360.
[100] Tuszynski, J.A.; Paul, R.; Chatterjee, R.; Sreenivasan, S.R.
Relationship
between Fröhlich and Davydov models of biological order. Phys. Rev. A, 1984, 30
(5), 2666-2675.
[101] Popp, F.-A.; Shen, X. The photon count statistic study on the photon
emission from biological systems using a new coincidence counting system. In:
Biophotons. Chang J.J.; Fisch J.; Popp F.-A., Eds.; Kluwer Academic Publishers:
Dordrecht, 1998; pp. 87-92.
[102] Gurwitsch, A.G.; Gurwitch, L.D. Die Mitogenetische Strahlung, ihre
Physikalisch-Chemischen Grundlagen und ihre Anwendung in Biologie und Medizin.
Gustav Fischer Verlag,: Jena, 1959.
[103] Popp, F.-A.; Chang, J.J. The physical background and the informational
character of biophoton emission. In Biophotons. Chang J.J.; Fisch J.; Popp
F.-A., Eds. Kluwer Academic Publishers: Dordrecht, 1998, 238-250.
[104] Popp, F.-A. About the coherence of biophotons. In Macroscopic Quantum
Coherence. Sassaroli E.; Srivastava Y., Swain J.; Widom A., Eds.; World
Scientific: New Jersey, London, 1998; pp. 130-150.
[105] Shen, X.; Van Wijk, R. Biophotonics: Optical Science and Engineering for
the 21st Century. Springer: New York, 2005.
[106] Del Giudice, E; Stefanini, P; Tedeshi, A; Vitiello, G.
The interplay of biomolecules and water at the origin of the active behavior of living organisms.
J. Phys.: Conf. Ser., 2011, 329, 012001.
[107] Ingber, D.E.
Tensegrity I. Cell structure and hierarchical systems
biology. J. Cell Sci., 2003, 116 (Pt 7), 1157-1173.
[108] Ingber, D.E.
Tensegrity II. How structural networks influence cellular
information processing networks. J. Cell Sci., 2003, 116 (Pt.8), 1397-1408.
[109] Jaeken, L.
A new list of functions of the cytoskeleton. IUBMB-Life, 2007,
59 (3), 127-133.
[110] Athenstaedt, H.
Pyroelectric and piezoelectric properties of Vertebrates.
Ann. N. Y. Acad. Sci., 1974, 238 (1), 68-94.
[111] Clegg, J.S.
Intracellular water and the cytomatrix: some methods of study
and current views. J. Cell Biol., 1984, 99 (1 Pt.2), 167s-171s.
[112] Abbott, D.; Davies, P.C.W.; Pati, A.K. (Eds.) Quantum Aspects of Life.
Imperial College Press: London, 2008.
[113] Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.-K.; Man.al, T.; Cheng,
Y.-C.; Blankenship, R.E.; Fleming, G.R.
Evidence for wavelike energy transfer
through quantum coherence in photosynthetic systems. Nature, 2007, 446 (7137),
782-786.
[114] Lee, H., Cheng, Y.C.; Fleming, G.R.
Coherence dynamics in photosynthesis:
protein protection of excitonic coherence. Science, 2007, 316 (5830), 1462-1465.
[115] Mercer, I.P.; El-Taha, Y.C.; Kajumba, N.; Marangos, J.P.; Tisch, J.W.;
Gabrielsen, M.; Cogdell, R.J.; Springate, E.; Turcu, E.
Instantaneous mapping of
coherently coupled electronic transitions and energy transfers in a
photosynthetic complex using angle-resolved coherent optical wave-mixing. Phys.
Rev. Lett., 2009, 102 (5), 057402.
[116] Collini, E.; Wong, C.Y.; Wilk, K.E.; Curmi, P.M.; Brumer, P.; Scholes,
G.D.
Coherently wired light-harvesting in photosynthetic marine algae at ambient
temperature. Nature, 2010, 463 (7281), 644-647.
[117] Plankar, M.; Jerman, I.; Krašovec, R.
On the origin of cancer: can we
ignore coherence? Prog. Biophys. Mol. Biol., 2011, 106 (2), 380-390.
[118] Keynes, R.D.; Maisel, G.W.
The energy requirement for sodium extrusion
from a frog muscle. Proc. R. Soc. Lond. B Biol. Sci., 1954, 142 (908), 383-392.
[119] Conway, E.J.; Kernan, R.P.; Zadunaisky, J.A.
The sodium pump in skeletal
muscle in relation to energy barriers. J. Physiol., 1961, 155 (2), 263-279.
[120] Minkoff, L.; Damadian, R.
Caloric catastrophe. Biophys. J., 1973, 13 (2),
167-178.
[121] Miseta, A.; Somoskeoy, S.; Galambos, C.; Kellermayer, M.; Wheatley, D.N.;
Cameron, I.L. Human and dog erythrocytes: relationship between cellular ATP
levels, ATP consumption and potassium concentration. Physiol. Chem. Phys. Med.
NMR, 1992, 24 (1), 11-20.
[122] Wheatly, D.N.; Miseta, A.; Kellermayer, M.; Galambos, C.; Bogner, P.;
Berenyi, E.; Cameron, I.L. Cation distribution in mammalian red blood cells:
interspecies and intraspecies relationships between cellular ATP, potassium,
sodium and magnesium concentrations. Physiol. Chem. Phys. Med. NMR, 1994, 26
(1), 111-118.
[123] Bogner, P.; Nagy, E; Miseta, A.
On the role of Na,K-ATPase: a challenge
for the membrane-pump and association-induction hypotheses. Physiol. Chem. Phys.
Med. NMR, 1998, 30 (1), 81-87.
[124] Nanninga, L.B.; Mommaerts, W.F.H.M.
On the binding of adenosine triphosphate by actomyosin. Proc. Natl. Acad. Sci. USA, 1957, 43 (6), 540-542.
[125] Asakura, S.
The interaction between G-actin and ATP. Arch. Biochem.
Biophys., 1961, 92 (1), 140-149.
[126] Ling, G.N.
The physical state of water and ions in living cells and a new theory of the
energization of biological work performance by ATP. Mol. Cell. Biochem.,
1977, 15 (3), 159-172.
[127] Eisenberg, E.; Hill, T.L.
Muscle contraction and free energy transduction
in biological systems. Science, 1985, 227 (4690), 999-1006.
[128] Irving, M. Weak and strong crossbridges. Nature, 1985, 316 (6026),
292-293.
[129] Vale, R.D.; Oosawa, F.
Protein motors and Maxwell's demons: does
mechanochemical transduction involve a thermal ratchet? Adv. Biophys., 1990, 26,
97-134.
[130] Post, R.L.; Toda, G.; Kume, S.; Taniguchi, K.
Synthesis of adenosine triphosphate by way of potassium-sensitive phosphoenzyme of sodium, potassium
adenosine triphosphatase. J. Supramol. Struct., 1975, 3 (5-6), 479-497.
[131] Leo, A.; Hansch, C.; Elkins, D.
Partition coefficients and their uses. Chem. Rev., 1971, 71 (6), 525-616.
[132] Matveev, V.V.
Protoreaction of protoplasm. Cell Mol. Biol. (Noisy-le-grand), 2005, 51 (8),
715-723.
[133] Yuan, Z.; Cai, T.; Tian, J.; Ivanov, A.V.; Giovannucci, D.R.; Xie, Z.
Na/K-ATPase tethers phospholipase C and IP3 receptor into a calcium-regulatory
complex. Mol. Biol. Cell, 2005, 16 (9), 4034-4045.
[134] Clegg, J.S. Intracellular water, metabolism and cell architecture. In
Coherent Excitations in Biological Systems; Fröhlich H.; Kremer F., Eds.;
Springer-Verlag: Heidelberg, 1983; pp. 162-177.
[135] Janmey, P.A.
The cytoskeleton and cell signalling: component localization
and mechanical coupling. Physiol. Rev., 1998, 78 (3), 763-781.
[136] Jaeken, L. In vivo protein unfolding and the ion pumping activities of the
cytoplasm: a claim for the association-induction hypothesis of G.N. Ling. Biochem. Bull., 2003, 2 8.
[137] Porter, K.R. The cytomatrix: a short history of its study. J. Cell Biol.,
1984, 99, (1 Pt.2), 3s-12s.
[138] Mirsky, A.E.; Pauling, L.
On the structure of native, denatured and
coagulated proteins. Proc. Natl. Acad. Sci. USA, 1936, 22 (7), 439-447.
[139] Mirsky, A.E.
Protein coagulation as a result of fertilization. Science,
1936, 84 (2189), 333-334.
[140] Mirsky, A.E.
The visual cycle and protein denaturation. Proc. Natl. Acad.
Sci. USA, 1936, 22 (2), 147-149.
[141] Dunker, A.K.; Lawson, J.D.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh,
J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; Ausio, J.;
Nissen, M.S.; Reeves, R.; Kang, C.; Kissinger, C.R.; Bailey, R.W.; Griswold,
M.D.; Chiu, W.; Garner, E.C.; Obradovic, Z.
Intrinsically disordered protein. J.
Mol. Graph. Model., 2001, 19 (1), 26-59.
[142] Uversky, V.N.
Natively unfolded proteins: a point where biology waits for
physics. Protein Sci., 2002, 11 (4), 739-756.
[143] Prokhorenko, D.V.; Matveev, V.V.
The significance of non-ergodic property of statistical mechanics systems for
understanding resting state of a living cell. Brit. J. Math. & Comput. Sci.,
2011, 1 (2), 46-86.
[144] Prigogine, I. Introduction to Thermodynamics of Irreversible Processes,
3rd ed. Interscience: New York, 1967.
[145] Rayment, I.; Holden, H.M.
Myosin subfragment-1: structure and function of
a molecular motor. Curr. Opin. Struct. Biol., 1993, 3 (6), 944-952.
[146] Pollack, G.H. Muscles and Molecules: Uncovering the Principles of
Biological Motion. Ebner & Sons Publ., Seattle, 1990.
[147] Page, M.J.; Di Cera, E.
Role of Na+ and K+ in enzyme
function. Physiol. Rev., 2006, 86 (4), 1049-1092.
[148] Ling, G.N.
Synchronous control of metabolic activity by K+
transiently and reversibly liberated from adsorption sites during muscle
contraction: an extension of association-induction theory. Physiol. Chem. Phys.,
1981, 13 (6), 565-566.
[149] Kachmar, J.F.; Boyer, P.D.
Kinetic analysis of enzyme reactions. II. The
potassium activation and calcium inhibition of pyruvic phosphoferase. J. Biol.
Chem., 1953, 200 (2), 669-682.
[150] Oria-Hernández, J.; Cabrera, N.; Pérez-Montfort, R.; Ramírez-Silva, L.
Puruvate kinase revisited: the activating effect of K+. J. Biol.
Chem., 2005, 280 (45), 37924-37929.
[151] Lowry, O.H.; Passonneau, J.V.
Kinetic evidence for multiple binding sites
on phosphofructokinase. J. Biol. Chem., 1966, 241 (10), 2268-2279.
[152] Suelter, C.H. Enzymes activated by monovalent cations. Science, 1970, 168
(933), 789-795.
[153] Kimmich, G.A.; Rasmussen, H.
Inhibition of mitochondrial respiration by
loss of intra-mitochondrial K+. Biochim. Biophys. Acta, 1967, 131
(3), 413-420.
[154] Moore, C.; Pressman, B.C. Mechanism of action of valinomycin on
mitochondria. Biochem. Biophys. Res. Commun., 1964, 15 (6), 562-567.
[155] Garlid, K.D.; Paucek, P.
Mitochondrial potassium transport: the K+
cycle. Biochim. Biophys. Acta, 2003, 1606 (1-3), 23-41.
Full text [PDF]